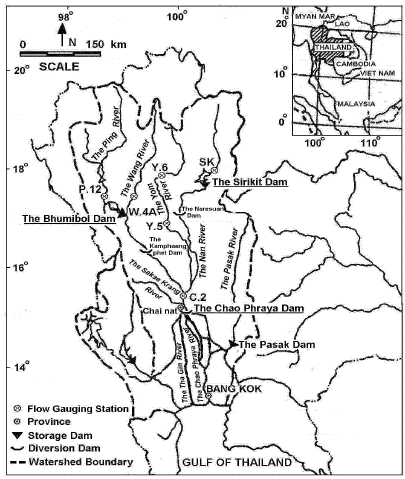
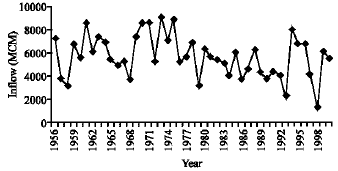
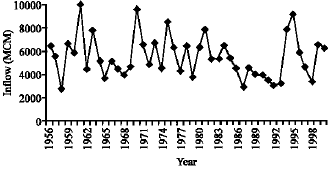
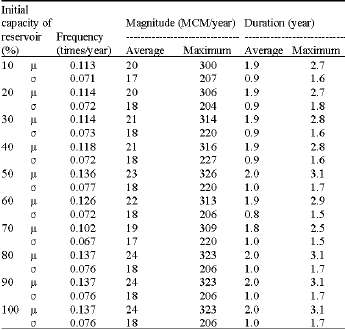
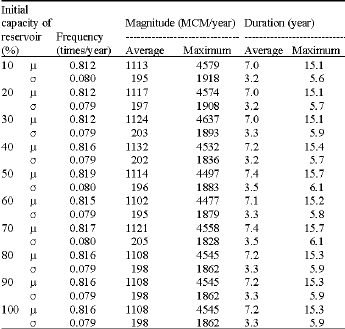
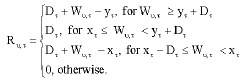Research Article
Suitable Conditions of Reservoir Simulation for Searching Rule Curves
Department of Civil Engineering, Faculty of Engineenng, Thammasat University Klong Luang, Pathumtham 12120, Thailand
Chavalit Chaleeraktrakoon
Department of Civil Engineering, Faculty of Engineenng, Thammasat University Klong Luang, Pathumtham 12120, Thailand