Research Article
Optimizing Multi-Product Multi-Constraint Inventory Control Systems with Stochastic Replenishments
Department of Industrial Engineering, Iran University of Science and Technology, Iran
Mir-Bahador Aryanezhad
Department of Industrial Engineering, Iran University of Science and Technology, Iran
Seyed Taghi Akhavan Niaki
Department of Industrial Engineering, Sharif University of Technology, Iran









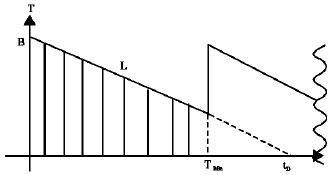
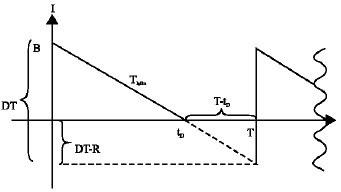
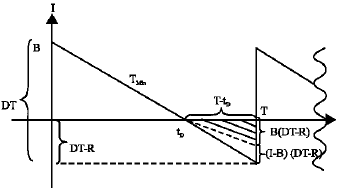
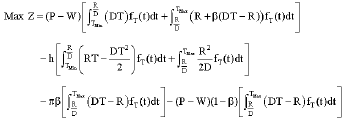

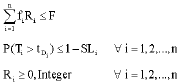
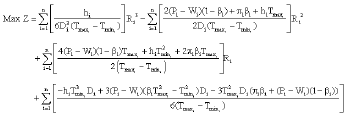
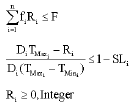
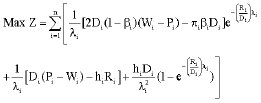


Seyed Taghi Akhavan Niaki Reply
How come this paper has not been indexed in Scopus yet?