Research Article
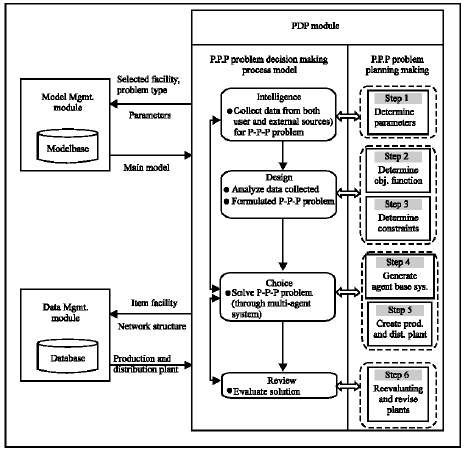
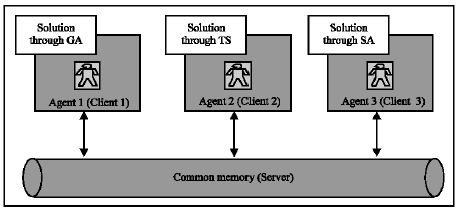
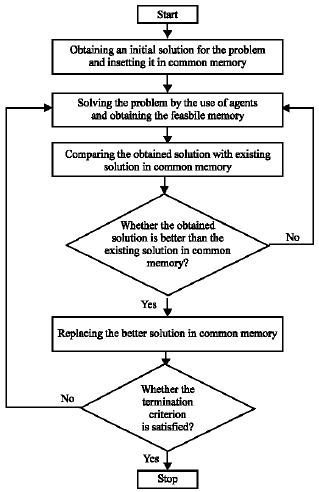
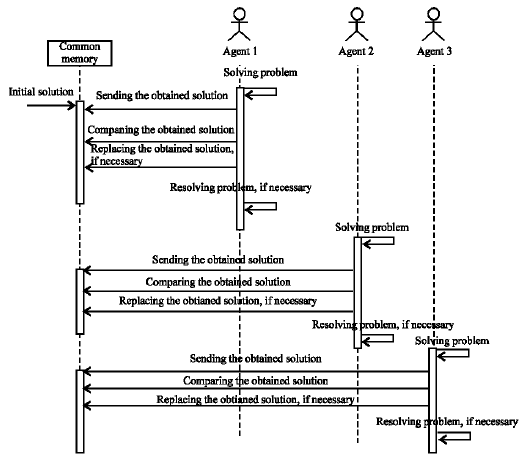
An Agent-Based Framework for Building Decision Support System in Supply Chain Management
Department of Industrial Engineering, Amirkabir University of Technology, P.O. Box 15875-4413, Tehran, Iran
M.H. Fazel Zarandi
Department of Industrial Engineering, Amirkabir University of Technology, P.O. Box 15875-4413, Tehran, Iran