Research Article
Physic-Based Imaginary Potential and Incoherent Current Models for RTD Simulation Using Optical Model
Shahid Beheshti University, Velanjak, Tehran, Iran
Keivan Navi
Shahid Beheshti University, Velanjak, Tehran, Iran
In recent years, advances in technologies such as MBE have made it possible to fabricate very small devices with dimensions comparable to the Debye’s length. As a consequence of this small dimensions, the I/V characteristics of such devices must be calculated by quantum theories. Among these devices, there are devices such as Resonant Tunnelling Diodes (RTD) which due to long dwelling time of their electrons inside the device, the scattering phenomena have a major rule in their operation and as a consequence, a ballistic quantum transport theory will not be adequate.
Unfortunately, the problem of quantum electron transport in presence of scattering phenomena is a hard problem and there is not yet an exact formulation for it. In this situation, a simple approximate formulation known as optical model attracted much attention. In the optical model, the effects of scattering phenomena are introduced by an imaginary potential into the Schrödinger equation (Schiff, 1968):
(1) |
In this formula, V is the real and w is the imaginary potential. This method has been used by many authors for simulation of RTD. Some of them (Hu and Stapleton, 1993) have used it directly through the Schrödinger equation as explained in the Eq. 1 . Others have used it via a path integral method (Zohta, 1990a, b; Zohta and Ezawa, 1992) or in conjunction with the Febry-Perot resonator (Furuya et al., 1994) or by transfer matrix or scattering matrix method (Yuming, 1988; Zohta, 1993; Zohta and Ezawa, 1992). All these approaches were successful and ended into similar results but there are two ambiguities common to all of them.
The first ambiguity is related to the amount of the imaginary potential that is needed in the calculations. The second ambiguity is related to the incoherent current which eventually flows through the device. The optical model itself says nothing about these two problems and we must use additional theories and models to clarify them.
PHYSIC-BASED IMAGINARY POTENTIAL FOR RTD
Determining the imaginary potential profile is the first step in the usage of optical model. Nevertheless, many papers have taken it as an unknown parameter and simply introduced their results for some different values (Hu and Stapleton, 1991; Zohta, 1990b; Hu and Stapleton, 1993). Some other papers that have tried to calculate it on a physical base, considered it simply as a scalar (a single number) (Zohta and Tanamoto, 1993). Here we will consider it in more detail and calculate it in its complete form with complete dependency of its bias, energy, position and temperature.
A simple form of imaginary potential can be obtained from mobility. Let us consider this simple form before going into details. By calculating the divergence of coherent current density (the current density from the Schrödinger equation when there exists an imaginary potential in the equation) using Eq. 1 and its complex conjugate, we have:
(2) |
Comparing this term with the classical formula for ∇.j in the case G = 0 yields (R is the recombination and G is the generation term):
(3) |
Considering the above relation and the relation existing between the carrier’s lifetime and the recombination term, R = n/τ, we get w = ħ/2τ (n is the carrier density which is equal to Ψ*Ψ and τ is the carrier’s lifetime). Now if we use the mobility formula, μ = qτ/m*, to substitute the carrier’s lifetime, we reach the desired relation between the imaginary potential and mobility:
(4) |
As a numerical example, for GaAs with m* = 0.067m0 and μ = 7500 at 300k the imaginary potential got from the above mentioned procedure will be equal to 1.8E-22. Nevertheless, the resulted imaginary potential is a scalar and is over simplified because mobility is only a low field averaged quantity and as it will be seen later, the real situations are more complicated.
To obtain a better estimation for the imaginary potential, we can use the scattering rates to estimate the carrier’s lifetime instead of using the mobility:
(5) |
In the above formula, the summation is over the scattering rates of various phenomena involved in the motion of electron and Etot is the electron’s total energy. For electrons in the RTD’s well, it is sufficient to include the scattering rates from the absorption and emission of polar optical phonons that cause electrons to scatter inside the gamma valley or from gamma valley to L valleys and the scattering rate from the acoustic phonons (totally 5 scattering phenomena). Scattering rates formulas are so long that we do not want to repeat them here. The reader interested in this issue may refer to appendix M of the reference (Singh, 1993). Figure 1 shows the results of those that have calculated for GaAs at 300 K. It shows the five mentioned scattering rates as a function of the electron’s total energy. The total energy can be calculated using the following formula:
(6) |
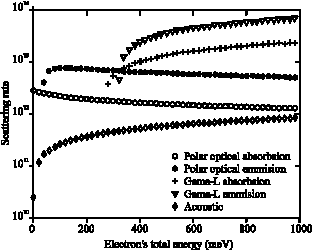 | |
| Fig. 1: | Electron’s scattering rates in the gamma valley of GaAs at T = 300K as a function of its total energy |
 | |
| Fig. 2: | Imaginary potential obtained from the Eq. 7 (black circles) as a function of position along the RTD’s well for T = 300K at different biases (from 0V to 0.5V) and different wave-vectors (corresponds to different electrons at the contact) in comparison with the imaginary potential obtained from the mobility (solid line) |
In this formula, the first term is the kinetic energy of electron at the contact. The second term is due to two electron’s transverse degrees of freedom and the third term is due to the potential energy. The imaginary potential finally becomes:
(7) |
The imaginary potential term calculated in this way has its full dependency on bias (via third term in Eq. 6), position (also via the third term of Eq. 6) and temperature (via second term of Eq. 6) and obviously is more reliable than a simple scalar term.
To show the scale of changes of the imaginary potential made by our model, we drew Fig. 2. In this figure, the horizontal axis is the position axes along the RTD’s well. The imaginary potential for different biases in the range of 0 V to 0.5 V and for different values of wave vector at the contact has been calculated and drawn on the figure. Also on the figure, the value obtained from mobility (Eq. 4) has been shown. We see the imaginary potential is not at all a single value and may vary very widely in different cases. We also see that the estimation obtained from the mobility is a very poor estimation.
INCOHERENT ELECTRON CURRENT IN RTD
When the imaginary potential term is added to the Schrödinger equation, the divergence of the current density is no longer equal to zero (Eq. 2) and the sum of the squared terms of transmission coefficient and reflection coefficient on the left side of the device is no longer equal to unity (Zohta, 1993):
(8) |
The difference is due to the scattering phenomena which take some of the incoming electrons from their in-phase (coherent) wave functions and scatter them into random phase (incoherent) states. These scattered electrons eventually make the incoherent current term that different opinions have been presented about it.
Some authors (Yuming, 1988; Hu and Stapleton, 1991) take the coherent current on the left side of the device as the total electron current (coherent current plus incoherent current). They have actually supposed that all scattered electrons finally go out from the well through only the right barrier and towards the right direction. Other authors (Zohta, 1993; Zohta and Ezawa, 1992; Zohta and Tanamoto, 1993) take not all but a portion of the ![]() term as the incoherent current term. They have actually supposed that a portion of the scattered electrons in the well eventually go through the right barrier and others go through the left one.
term as the incoherent current term. They have actually supposed that a portion of the scattered electrons in the well eventually go through the right barrier and others go through the left one.
In a previous study (Sharifi, 1999), we explained that the scattering phenomena cause the electrons to become incoherent with the incoming electrons, but they don’t cause them to become classical particles having no phase and wave nature. In other words, the scattered electrons must be considered as quantum particles either. Therefore assigning any property to the squared terms of the transmission coefficients of the right barrier and the left barrier separately as is the case in the references (Zohta and Ezawa, 1992; Zohta and Tanamoto, 1993), is not a correct assignment because this assignment will erase any interfering term between the two barriers.
Therefore we suggest to use the meta-stable states for modelling of the scattered electrons. Meta-stable states are the states of a system when its boundary conditions are set in such a way that they show only outgoing electrons from all the boundaries of the system. Therefore, the meta-stable states may model the trapped electrons in the well of RTD which are gradually going out from both two barriers. Another point that supports the usage of the meta-stable states, is the fact that the density of states in the well of RTD has a big peak at the energy of these states; therefore, we expect most of the scattered electrons go to these states.
Further, we will calculate these states for RTD and in the section after that we will use them for calculation of the incoherent current.
AN APPROXIMATE ANALYTICAL METHOD FOR META-STABLE STATES OF RTD
In a previous work (Sharifi and Adibi, 1999), we had introduced a numerical method for calculating meta-stable states of RTD. Here we introduce an approximate analytical method. We begin by introducing an approximate potential profile using a WKB concept. This potential profile is constructed by replacing the two barriers with two impulse functions having the same area (Fig. 3).
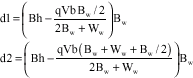 | (9) |
The d1 and d2 are the powers of the two impulse functions replaced the left and the right barriers, respectively. Bh is the barrier’s height. Bw and Ww are the barrier’s width and the well’s width, respectively and Vb is the applied bias voltage. For the wave function, we assume three proper combinations of exponential terms in the three regions (Fig. 3) (all ks are complex, E is complex too).
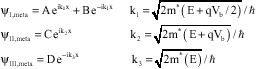 | (10) |
Let us to consider the zero bias condition at first (k1 = k2 = k3 = k). By equating the corresponding wave functions at the two sides of the two barriers, respectively and equating the difference of gradients of corresponding wave functions at two sides of two barriers with the corresponding integrals of the potential profile, we get the following relations:
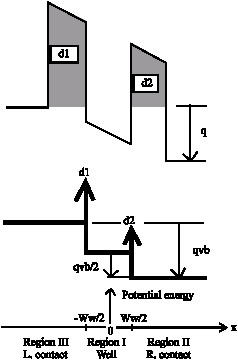 | |
| Fig. 3: | Potential profile of RTD (upper-graph) and its approximation by a stair shaped one with two impulse functions; d1 and d2 (lower-graph) |
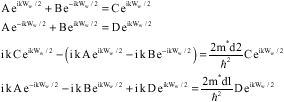 | (11) |
One of the four constants in the above four relations can be omitted from normalization concept. We selected it to be B and take it to be eikWw/2. Three other constants can then be calculated from the first three relations:
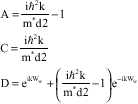 | (12) |
Inserting these constants into the last relation will give us the desired equation for k:
(13) |
| Table 1: | A few first meta-stable states energy’s Eigen-value for RTD at zero bias (The RTD’s parameters are the same as Fig. 4) |
 | |
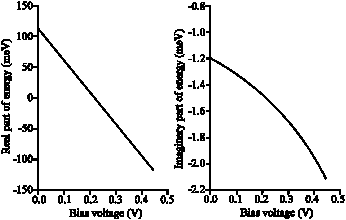 | |
| Fig. 4: | The real part (left plot) and the imaginary part (right plot) of Eigen-value of the first meta-stable state of RTD as a function of bias voltage calculated with the Eq. 15. The parameters are: Ww = 50A, Bw = 24A, Bh = 1eV |
This is a nonlinear multiple-answer algebraic equation which may be solved by a computer to get the answers for k. The Eigen-values for energy can then be calculated using
Table 1 shows a few first energy Eigen-values. Any of these Eigen-values has a negative imaginary part. This negative imaginary part causes the corresponding probability density function to decay in time as expected of a meta-stable state.
Now the procedure can extend to non-zero bias condition. It is lengthier but is straightforward and ends into the following equation.
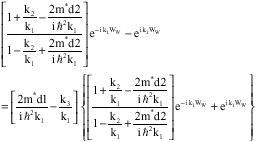 | (14) |
The k1, k2 and k3 may be replaced with their definitions in the Eq. 10 to obtain an equation for energy. Again, the equation is a nonlinear multiple-answer complex equation which can be solved using a computer. Figure 4 shows the result for the first meta-stable state energy’s Eigen-value, as a function of bias voltage. We see the real part has almost a linear functionality of the bias but the imaginary part has a more complex functionality. After calculating the complex Eigen-value; E, the complex wave vectors, k1, k2 and k3 may be calculated from Eq. 10 and then the constants A, C and D may be calculated from an extension form of the Eq. 12. We need these quantities for calculating the incoherent current at the next section.
INCOHERENT CURRENT MODEL USING META-STABLE STATES
For incoherent current, we suggest the following formula (in the formula 0 is the left hand side of the device, L is the right hand side and x is a middle point inside the device.):
jincoh (x) = (jcoh (0) - jcoh (x)) Tsr - (Jcoh (x) - jcoh (L))Tsl | (15) |
This formula has a clear interpretation. As mentioned before in optical model, the divergence of coherent current density is related to the scattering rate of electrons (Eq. 2). Therefore the integral of that term from 0 to x which is the coherent current density itself is equal to the total scattering rate in the interval [0, x]. In Eq. 15, this integral is multiplied by Tsr, which is the transmission to right coefficient to yield the positive term of our incoherent current density. In the same manner, the total electrons scattered in the interval [x, L] is multiplied by Tsl (the transmission to left coefficient) to yield the negative term of the incoherent current.
The two parameters, Tsr and Tsl, may be calculated by the following relations using the before mentioned meta-stable states:
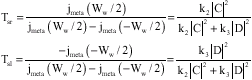 | (16) |
Tsr and Tsl as calculated above are no longer local parameters due to the transmission coefficients of the two barriers separately, but are global parameters that preserve all interference terms that may exist between the two barriers. Therefore the introduced model preserves the wave nature of incoherent electrons as well. Figure 5 shows the calculated Tsr as a function of bias. In the figure, the lines Tsr = 1 and Tsr = 0.5 have also been plotted which the first line corresponds to those papers (Yuming, 1988) that supposed all scattered electrons will eventually go to the right. The second line corresponds to those (Zohta, 1993) that supposed a half of scattered electrons will go to the right. From the figure, we see that the result obtained from meta-stable states is close to the results of the first papers at high biases and to the second papers at low biases. This is a very good behaviour that matches our expectations and now is obtained nicely from a firm physical base.
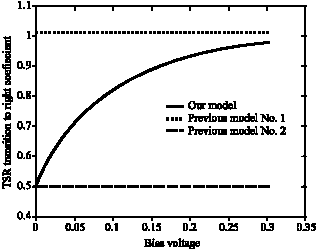 | |
| Fig. 5: | |
The incoherent current as suggested by Eq. 15 has an interesting aspect. Divergence of total current, if its incoherent term is calculated by that equation, will be equal to zero in agreement with the particle conservation concept.
(17) |
THE ALGORITHM AND THE RESULTS
In our model, the current-voltage characteristics of RTD can be calculated in the following steps:
| • | Calculate the Fermi level and then the potential profile by solving the Poisson’s equation using the impurity profile of all device layers including buffer, spacer and contact layers. |
| • | Calculate the imaginary potential as a function of position for any bias and any (longitudinal) wave vector at the contact (Eq. 7). |
| • | Insert the potential profile from the first step and the imaginary potential from the second step into the Schrödinger equation. Solve it and calculate the coherent current profile for any wave vector at any bias point. |
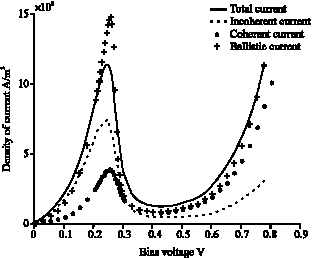 | |
| Fig. 6: | The coherent, incoherent and total current of RTD at T = 300K in conjunction with the ballistic current. The brief RTD’s parameters are: Well: 50 A GaAs; Barriers: 17 A AlGaAs; Barrier height: 0.65 eV; Contact doping: 1e18/cm3 |
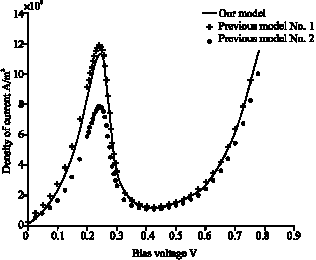 | |
| Fig. 7: | The results of our model for the total current of RTD in comparison with the two previous models (RTD’s parameters are the same as Fig. 6) |
| • | Calculate the meta-stable states and then Tsr and Tsl at any bias point using Eq. 9. |
| • | Calculate the incoherent current for any wave vector at any bias point using Eq. 15. |
| • | Calculate the total coherent, the total incoherent and the total current at any bias point by a summation over the corresponding the above partial terms weighted by density of states (Sharifi and Adibi, 1999). |
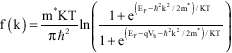 | (18) |
Figure 6 shows the total coherent, incoherent and total current in conjunction with the ballistic current (current, when there is no scattering). Figure 7 compares the results of our model for total current with the two previous models as mentioned before. The first previous model (No. 1) had supposed that all scattered electrons go eventually through the right barrier (Yuming, 1988). The second previous model (No. 2), on the other hand, had supposed that half of scattered electrons go through the right barrier (Zohta, 1993). We see the new results are closer but not equal to the model number 1.
In this study, we introduced two physic-based models, one for the imaginary potential and another for the incoherent current based on the meta-stable states. We then used these two models through the optical model for simulation of RTD and compared our results with the previous results. The two models introduced are not restricted to RTD and can be used in other quantum devices as well. Beside of the incoherent current, there is another important quantity that can be calculated from the meta-stable states too. This quantity is the incoherent electron density which its determination enables us to do a truly self consistent calculation. We believe by these two models, the optical model has gotten a better situation and in the future it will be used more than past.