Research Article
Regional Health Sector Performances in Tanzania: A Comparison of Various Aggregating Schemes
Department of Economics, University of Dar es Salaam, P.O. Box 35045, Dar es Salaam, Tanzania
Tanzania, like many other countries, publishes many indicators which measure the performance of the health sector at sub-national level (regional level). Health sector performance indicators are among other indicators used by the central government to guide budgetary resource allocation to local governments. However, these indicators are often not correlated, which makes it difficult to have an overall comparison of how one region perform contrary to other regions. For consistent policy interventions, it is necessary to have an indicator which is able to consistently rank the regions. One of the simple options is to create an aggregated index from the given statistics using some pre-determined indicators’ weights. Ideally however, these weights ought to be different from one region to another since different geo-physical environment dictates varied intensities of health problems. Thus, a uniform indicator’s weight applied across all regions may give a misleading status of the regional health performance.
The need to have a consistent ordering of the regional health performance is increasing in the era where more devolution of government operations is expected (Boex and Martinez-Vazquez, 2003). Such ordering will have direct policy implications on the nation and may provide necessary political pressure on local governments that could form a strong basis for bargaining for more budgetary resources.
One of the steps towards having the ordering of regional health performance is to identify the benchmark region for health index. Preparation of such a benchmark index is a well-established tool for measuring performance in business practice as well as the public sector organizations where comparative performance evaluations are regularly conducted (Cox and Thompson, 1998; Auluck, 2002). In theory, standard bench marking requires identification of peer regions, which exemplify best practice in health sector so that other regions are assessed in relation to this best performer. Unfortunately, unlike where indicators can readily be aggregated and then compared, aggregation of the indicators in the health sectors pose more methodological difficulties. These difficulties arise as a result of varied geo-physical environment and thus, different intensities of health problems. Therefore, a uniform indicator’s weight applied across all regions needs be avoided (Cherchye and Kuosmanen, 2002).
Borrowing from the methodology, which was initially used in environmental science and later, in comparing macroeconomic performance of various countries (Easterly et al. 1993; Cherchye, 2001), this paper develops a Unified Health Performance Index (UHPI) at the regional level in Tanzania. The index combines existing standard health performance indicators (e.g., mortality rates, HIV prevalence, etc.). Since each indicator individually provides useful but different information, the basic motivation for the paper is to combine and structure the information captured in the existing standard health performance indicators into a relative index that is able to rank the performance of each region in Tanzania. As Cherchye and Kuosmanen (2002) argue, simple aggregation method of various indicators is prone to arbitrary judgments and lacks subjectivity because it is not based on explicitly stated, scientifically sound premises.
In this study, we use a so-called benefit of the doubt weighting method as discussed in Carrington et al. (2002) and Cherchye and Kuosmanen (2002). The advantage of this approach is that, it avoids the problem of arbitrary weighting schemes (for a priori, it is not clear which health indicators are the most appropriate to evaluate). Under the benefit of doubt weighting scheme, the problem is solved such that at the optimal solution, higher weights are attached to those health indicator for which the region under evaluation performs relatively better. In similar spirit to how Data Envelopment Analysis (DEA) works, the program endogenously selects those weights that yield the best Unified Health Performance Index (UHPI) for each region under investigation (Cherchye, 2001). Initially this weighting scheme was introduced in ranking the macro economic performances (macro economic indicators) for various countries (Easterly et al., 1993; Cherchye, 2001).
CONSTRUCTION OF THE UNIFIED HEALTH SECTOR PERFORMANCE INDEX
Basic structure: In line with Carrington et al. (2002) and Cherchye and Kuosmanen (2002), we consider the case where there are m health performance indicators from n regions. Let yij be the value of the health indicator i in region j. As elaborated in the previous section, the aim is to merge these individual health indicators (i.e., for all i over j) into a single-valued index (UHPI over j). Based on the benefit-of-the-doubt weighting procedure, we assume ignorance of the true relative value of each health indicator when compared to the other health indicators in order to produce those weights that maximize the UHPI for each region. It should be noted that, the region-specific health indicator weights under the benefit-of-the-doubt procedures are the outcomes of an optimization problem such that the weighted sum of the region-specific health performance values is maximized (Cherchye and Kuosmanen, 2002).
For notational simplicity, let Ωj denote the UHPI for region j (other notations will be defined immediately as they appear for the first time in the equations). It follows from this argument that Ωj for region j is the weighted average given by Eq. 1.
| (1) |
where weights W*ij are obtained from the optimal solution to the following problem:-
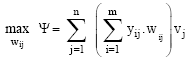 | (2) |
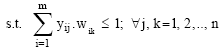 | (3) |
| (4) |
Equation 2 shows that weights for each region are endogenously selected to maximize the weighted sum of regional-specific health performance index values (UHPIs), where each region j (j = 1,.., n) is weighted by a priori specified weight vj. The unknown variables W*ij (i = 1, …., m; j = 1, …, n) represent the weight accorded to health performance indicator i for computing the Unified Health Index value (UHPI) for region j. Since the resulting UHPI is a relative index, we impose a scaling constraint in Eq. 3. This constraint ensures that no region can achieve unified index value that does exceed unity under the optimal weights. Equation 4 is the usual non-negativity restrictions in linear programming models. The non-negativity restrictions in Eq. 4 ensure that negative weights are excluded from the feasible solution. Cherchye and Kuosmanen (2002) show how the weights so determined could be interpreted as policy weights. However, we do not pursue this idea in this study.
Cherchye and Kuosmanen (2002) show that the program presented in Eq. 1 through 4 results in the highest relative weights being accorded to those health indicators for which region j performs best (in relative terms) when compared to other regions in the country. In Eq. 1; if Ωj = 1 it implies that there exists at least one weighting scheme under which region j yields the highest attainable unified index value over all other regions. Therefore, Ωj = 1 shows optimality relative to other regions. Otherwise, the region is considered suboptimal.
Extension of the basic structure: Both in theory and practice, it has been shown that the restrictions imposed in the weights W*ij may not be satisfactory (Thompson et al., 1993; Pedraja-Chaparro et al., 1997). This is because the restrictions imposed on the W*ij does not exclude extreme scenarios, where all the relative weight can be assigned to one health indicator (and ignoring the rest by assigning them a weight equal to zero). To avoid this problem, this paper follows the weight restriction approach suggested by Kuosmanen (2002). Although Kuosmanen (2002) initially intended to handle missing data problems (without affecting the results at the optimal point) we extend this approach and show that it can be used in cases where the reported health indicator is unrealistically too low or too high. Thus, in line with Kuosmanen (2002), we suppose that D is the index set of the extreme values we want to exclude in the weighting assignment. Then the restrictions (disjunctive constraints) are defined as follows.
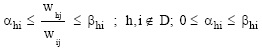 | (5) |
Since we essentially deal with linear model, Eq. 5 should be linearized to fit in our model. Linearizing Eq. 5 give the following pair of restrictions:
 | (6) |
Although the purpose of imposing additional restrictions on the optimal weights is to avoid the problem of extreme observations, this method has been criticized for choosing restrictions arbitrarily. Consequently, the opponents of this method argue that the obtained results are sensitive to the chosen restrictions (Allen et al., 1997). To avoid this problem of choosing the weighting restrictions arbitrarily, we follow the following strategies. First, because we want to keep with other (Allen et al., 1997), we start with the weight that is commonly used in DEA empirical literature by setting αhi = 0.1 and βhi = 10. This weight restrictions means that, for any given region, the maximum weight of any health indicator is at most 10 times greater than the minimum weight given to that indicator in any other region. Secondly, to test the robustness of our results, we extend the model such that αhi and βhi are generated from 1000 draws from uniform distributions specified as:
For each draw, we solve the model such that the results we present in the results section are the sample mean of results from the 1,000 simulations. Before we present the results, the next section briefly discusses the data used in this study.
DESCRIPTION OF THE DATA USED
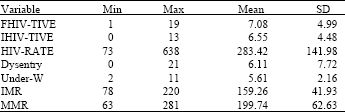
For the empirical analysis, the paper uses the regional cross-section data from various Health Statistics Abstract published by the Ministry of Health in Tanzania. We base our analysis on only 19 regions on Tanzania Mainland. The main reason for this is that there is no comparable data for the regions in Zanzibar and Dar es Salaam region is excluded because it has extreme values in some of the indicators, which could bias our results. Moreover, Dar es Salaam region misses a considerable amount of information needed for this model. We use the following indicators of (ill-) performance in health sector (in the parentheses are the variable labels used in the model): Percentage of family blood donors who tested HIV positive in 1996 (FHIV-TIVE); Percentage of institutional blood donors who tested HIV positive in 1996 (IHIV_TIVE); Cumulative rate of HIV positive per 100,000 of population for the period between 1992 and 1996 (HIV_RATE); Number of death caused by dysentery in 1995 (DYSENTERY); Percentage of underweight children aging less than five years in 1997 (UNDER-W); Infant and Under 5 Child Mortality Rate in 1995 (IMR); Maternal Mortality Rate in 1995 (MMR).
Table 1 summarizes the common descriptive statistics of these variables for Tanzania, i.e., at the national level. As expected, it is evident that the mean of most of these variables are relative high when compared to the world average. However, they do not differ substantially from those in the African region south of Sahara.
Table 2 presents the pair-wise correlation between the above listed performance indicators of health sector. It is apparent that there is no clear correlation pattern on the indicator across regions. Furthermore, it is evident that there is quite low correlation in these variables, which implies that simple aggregation for the purpose of getting regional rankings could be quite misleading.
| Table 1: | Selected descriptive statistics of Tanzania health indicators used in the model |
 | |
| Source: MoH (1999) | |
| Table 2: | Pair wise correlations of various health performance indicators in Tanzania |
 | |
| Source: Computed from MoH (1999) | |
In some cases, the correlation turns to be negative with relative large magnitudes. As will be shown later, the results from the index we estimate support our view that, simple ranking based on average of the simple ranks provides a somewhat misleading picture.
Note that, since all the indicators are ill-performance indicators, we take reciprocal of each indicator in order to conform to the maximization framework presented in Section 2. In case the variables have zero realization, we consider this as problem of data and consider it as missing. Note also that, as presented in Section 2, all health performance indicators are important and we would want to leave enough room for the benefit of the doubt interpretation (i.e., a conservative approach as emphasized by Cherchye and Kuosmanen (2002).
RESULTS OF THE UNIFIED HEALTH PERFORMANCE INDEX
This section presents and discusses the results of the model that ranks the performance of the health sectors across all regions of Tanzania Mainland (except Dar es Salaam region which has been excluded for technical reasons elaborated in the previous section). We first present the results of the model where the maximum allowed weight is fixed. Then we present the results where the maximum allowed weights are allowed to vary in a pre-determined interval. This second set of results allows us to test for the robustness of our ranking (based on the standard error of 1,000 simulations). Eventually, we compare the results of our model (i.e., the ranking of regions according to the performance of the health sector) with the results based on simple ordering.
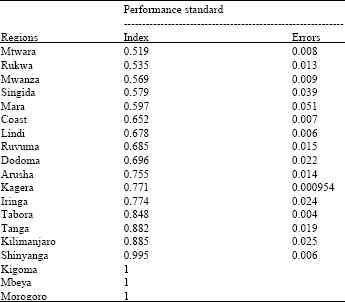
Result I: Maximum weight restricted to 10 times the minimum: When the weights are fixed such that the maximum weight cannot exceed ten times the minimum weight, we generally find that the majority of the regions perform above 0.5 in this index defined in the unit interval. It is worth to note that, four out of 19 regions happen to have the best performance. Among the best performers are Morogoro and Mbeya regions, whose substantial parts are mountainous; a feature which reduces the incidences of some diseases such as malaria.
| Table 3: | Regional health performance indexes and their respective standard errors regions |
 | |
| Source: Computed from MoH (1999) | |
Kigoma, which is among the best performer, has a unique feature in that it host a large number of the refugees from the turbulent states along the Greater Lake Zones. As a result of the presence of a large number of refugees, arguably the region has been receiving some health care from several international agents which other regions in the country do not receive (Roberts and Hofmann, 2004). In the lower tail of the performance ranking using this method are Rukwa and Mtwara regions. The position of these regions in this case is not astonishing because the same regions also rank low in terms of other indicators such as food and income poverty indexes and access to road infrastructure (NBS, 2002)
Result II: Random restriction in 10±5 interval: Table 3 presents the results when the restriction is now allowed to vary in the (5, 15) interval. Since the results are generated from a simulated model, we present the results in the form of the mean and standard deviations of 1000 simulations. It is apparent that results based on the simulations are quite similar to those obtained from a fixed parameter at the upper and lower end of the performance spectrum. Thus, the three regions that were observed to perform best are the same under these two different modeling frameworks. Likewise, the two regions that performed poorly are the same. In the mid of the spectrum, few regions were ranked differently under the two modeling frameworks.
Given the similarity in the two results, interest also lies in testing the robustness of the simulated results vs. those obtained using fixed parameters. To that end, we use the t-test to test whether the simulated results are significantly different from those obtained under fixed weight restriction. We generally find that efficiency scores are statistically different from those few regions for which the two modeling frameworks produced different ranks. However, the test of the correlation of the ranking is not statically different, which indicated that the basic model is as good as a model based in simulation. Thus, this study does not find evidence against using fixed parameter.
Comparison of endogenous ranking with simple ranking: When we compare the endogenous ranking of the regional performance in health sector with the simple average ranking, we find a drastically different picture. For example, we find that Morogoro region which ranked among the first under the endogenous ranking happen to hold the 10th position under the average of the simple ranking. Likewise, Singida region which ranked 12 based on the endogenous ranking but was ranked 4th under the simple rankings. The number of cases in which the simple ranking understates the performance of the region is 14 out of 19. In other words, the number of cases in which the simple ranking overstates the performance of the region is 4 and only one case in which the two ranks coincide.
Although the two ranking are different, we also wanted to establish whether these differences are statistically different. The estimated Spearman’s rank correlation between the average of the simple ranking and the index generated by our model is 0.4557. The p-value of the test of the null hypothesis that the value is statistically different from zero is 0.0499, which offer sufficient evidence that even the simple average of the ranks are close to those ranks generated by the endogenous ranking model.
SUMMARY AND CONCLUSIONS
This paper has discussed how multi-dimensional health performance indicators can be combined to generate a unified index which, if used consistently, can rank the performance of the regions. This index avoids the problem of using simple average of the ranks of the regions or seemingly arbitrary weights. The problem is avoided because our unified index is generated as an optimal solution, higher weights are attached to those health indicators for which the region under evaluation performs relatively well (similar to estimation of efficiency in Data Envelopment Analysis). This method has been used in ranking the macroeconomic performance of various countries and what this paper has done is to extend it in a way that avoids the use of fixed parameter (by using simulation method, where parameters are drawn from a uniform distribution of a pre-specified interval).
The results of the unified index happened to rank regions differently when compared with the ranking based on the simple average of the simple rankings. However, correlation between the rankings using this unified index showed relatively high correlation with the ranking based on simple average. Generally though, the policy implications in the two rankings are likely to be quite different.
It should be noted also that, further research is needed where one considers the indicators analyzed here as outcome (output) of a production process whose inputs are regional budgetary allocation to heath sector, available basic facilities (beds per regional population, physicians per population, etc.) and then analyses which regions are efficient in health productions using either parametric approaches (e.g., stochastic frontier) or non-parametric approaches (e.g., Data Envelopment Analysis). Furthermore, since much of the supervisions are carried at the district levels, future study could be much more policy-informing if carried at the district levels. But in any case, such kind of analysis should be able to control for variables that are beyond the control of the policy-implementers (such as population density, etc.)