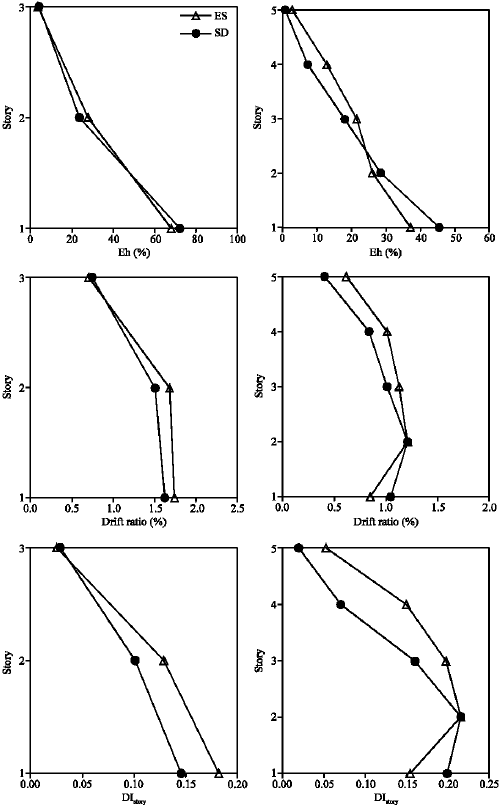
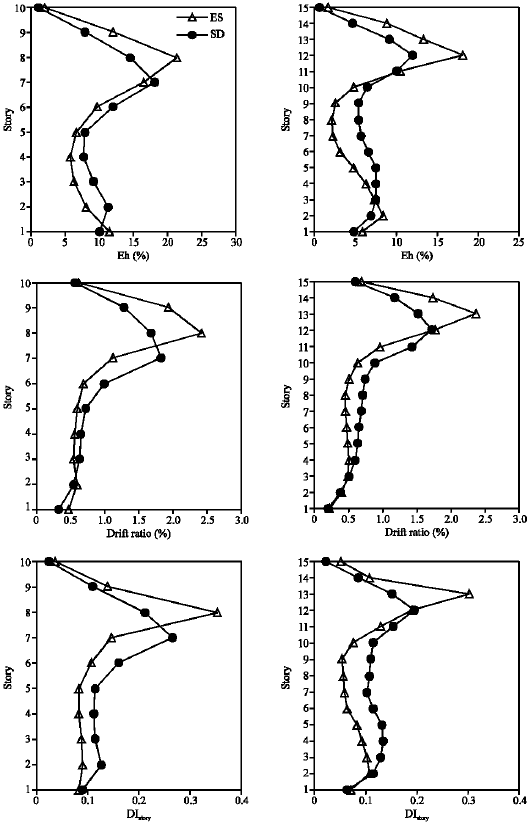
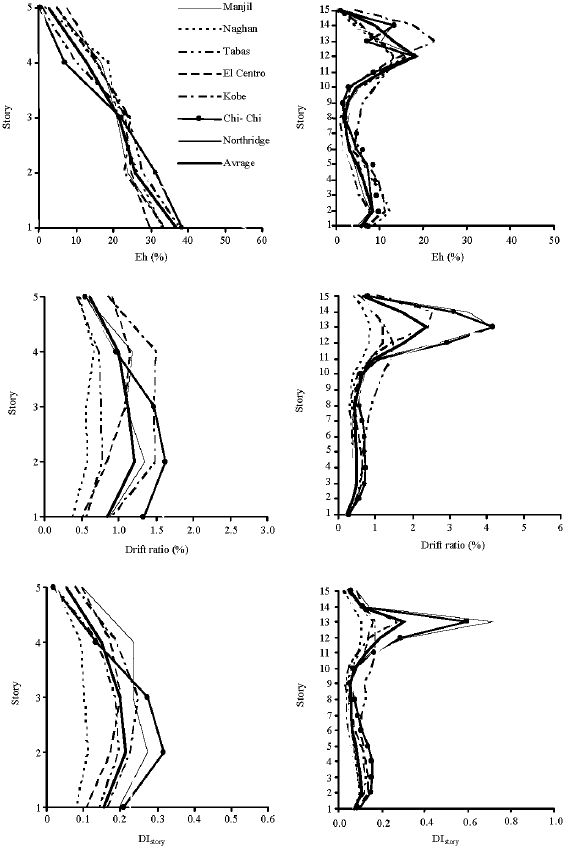
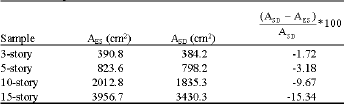
Research Article
Effect of Seismic Loading Patterns on Height-Wise Distribution of Drift, Hysteretic Energy and Damage in Reinforced Concrete Buildings
Department of Civil Engineering, Faculty of Engineering, Mazandaran University, Shariati Avenue, P.O. Box 47144-484, Babol, Iran
J. Vaseghi Amiri
Department of Civil Engineering, Faculty of Engineering, Mazandaran University, Shariati Avenue, P.O. Box 47144-484, Babol, Iran
G. Ghodrati Amiri
Center of Excellence for Fundamental Studies in Structural Engineering, College of Civil Engineering, Iran University of Science and Technology, P.O. Box 16765-163, Narmak, Tehran 16846, Iran
S.A. Razavian Amrei
College of Civil Engineering, Iran University of Science and Technology, P.O. Box 16765-163, Narmak, Tehran 16846, Iran