ABSTRACT
This study reports the results of the derivation of the equation of the contraction of a rain drop in space as it moves in the gravitational field of a stationary homogeneous prolate spheroidal body. It highlights the issue of the universe being in dynamic equilibrium, unlike Einsteins viewpoint that adopts the Doppler effect for the explanation of cosmology.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2007.3330.3333
URL: https://scialert.net/abstract/?doi=jas.2007.3330.3333
INTRODUCTION
It is well known that for five and a half decade of years ago, the theoretical investigation and experimental research for the solutions of a contraction of the length of a pendulum clock in the gravitational fields were limited almost exclusively to the fields of massive bodies of perfectly spherical geometry. But beginning from 1952 to date (Harold, 1952; Vinti, 1959; Howusu and Uduh, 2003; Howusu and Musongong, 2003; Musongong and Huwusd, 2004a, b) it has become increasingly recognized that the Earth, the Sun as well as almost all major astronomical bodies including raindrops in the atmosphere are actually oblate spheroidal or prolate spheroidal and their geometry has experimental, measurable and physical and interesting effects on the motion of test particles in their gravitational fields and as well as other corrections. For a simple reason, all measurements give dimensionless numbers, since the outcome of their results is often checked by units defined by other measurements. Length, for instance is measured by comparing the space between coordinates which Einsteins analysis has paved the way to accelerated coordinate system and has led directly to the idea that space-time is curved and that curvature is the origin of gravitation (Lars, 1986). Gravitation gives rise to gravitational length contraction as a body moves in space exterior to a stationary homogeneous spherical massive body according to his geometrical theory known as General Relativity (Nightingale et al., 1979). This results in a physically undefined Curvature or bending of space-time around a massive body. The bending of space has led to the greatest controversy in the field of science that the universe is expanding, contracting or in a state of dynamic equilibrium. Whichever way one looked at the matter, experimental results to prove the above issue should be the only deciding factor. As at now results available so far cannot lay claims, which model, should be adopted but for a near fact because such results should give an account of the size before, what size is it today and to what size will it last and when?
In 1915, Einstein had finishing touches to his General Relativity Theory (GRT). One of his famous solutions was that of Robertson and Walker (Islam, 1992) which has the significant of explaining Cosmology and any other spectral shifts in the Solar system. It is worth mentioning that these solutions alongside with the Einstein’s field equation looked rather cumbersome to kinder garden students of physics and professors of physics. The Robertson-Walker metric or line element is fundamental in the standard of Cosmology model as of today. The mathematical framework in which R-W metric occurs is that of Relativity and takes the form:
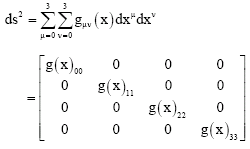 | (1) |
This can further be written as:
 | (2) |
Where:
| (3) |
and R(t) is the scale factor of the universe often personalized to be called the expansion factor and has the dimension of length, k can have values of k = 0, 1, -1 corresponding to different kinds of metrics.
In General Relativity among the important quantities, that one has to calculate is Ricci tensor defined as follows (Landau and Lifshitz, 1980):
| (4) |
where, Γ is the Christoffel symbols or affine connection of second kind which are defined by:
| (5) |
The Ricci tensor finally leads to the GRT field equation defined by:
| (6) |
where, ![]() is the Kronecker delta function and
is the Kronecker delta function and
| (7) |
are the diagonal elements of the energy momentum tensor in the case of a vacuum. For other medium different from vacuum, Tμv ≠ 0, but derived with respect to the medium. These equations and their solutions have formed the basis of the hitherto resolved natural phenomena of anomalous orbital precession, gravitational shift of spectral lines, gravitational time dilation, the radar sounding and geodetic deviation in the solar system as well as the still contended gravitational length contraction as it applies to a rain drop whose geometry has hitherto grave contributions in its motion and has led to our investigations.
 | |
| Fig. 1: | A prolate spheroidal massive body |
We have studied the above model though cumbersome, the idea motivated us to theoretically investigate the contraction of length of a rain drop (way A prolate spheroidal massive body of making the above subject easier and understandable) in space it moves exteriorly to a stationary homogeneous massive prolate spheroidal body such as an astronomical body of gravitational potential Φg.
THEORETICAL ANALYSIS
Consider a homogenous massive prolate spheroidal body of surface parameter ξ0 and rest mass M0 as shown in Fig. 1.
The prolate spheroidal coordinates of space (η, ξ, φ) are defined (Arfken, 1968; Hildebrand, 1962) in terms of the Cartesian coordinates (x, y, z) as:
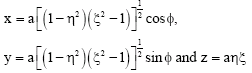 | (8) |
where, a is a constant, η is adjustable as the rain drop transverse space and 0≤ξ≤4, 0≤φ≤2π and the surface is given by the equation ξ = ξ. Let xμ be the Cartesian coordinates and ![]() corresponding prolate spheroidal coordinates of flat space-time given by:
corresponding prolate spheroidal coordinates of flat space-time given by:
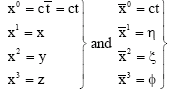 | (9) |
where, c is the speed of light in vacuo. It therefore follows from definition and the invariance of the world line element ds2 and proper time interval dτ as:
| (10) |
Equation 10 by invariance of the proper time reduces to:
| (11) |
where, τ is the proper time interval in prolate spheroidal coordinate.
Also the metric tensor in prolate spheroidal coordinate ![]() are defined by the relation:
are defined by the relation:
| (12) |
It is well known that when a photon is created in a potential well (rain drop) with gravitational potential ![]() , a mass of Δm1 is converted to photon energy (Wesley, 1996) such that:
, a mass of Δm1 is converted to photon energy (Wesley, 1996) such that:
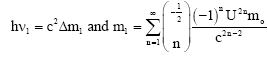 | (13) |
Where:
| h | = | The Planck constant, |
| mo | = | Rest mass and |
| v | = | The photon frequency. |
After the photon is absorbed at a higher gravitational potential Φ2g, its energy hv2 is converted to mass Δm2 such that:
| (14) |
Consequently, following the conservation of energy including the gravitational potentials, we have
| (15) |
and hence the change in frequency Δv is given by
| (16) |
For an observer on earth or on the body of a prolate spheroid such as raindrops, the final potential Φ2 ≈ 0 which is at infinity relative to a star or the other bodies. Hence:
| (17) |
while dropping the subscripts.
Now, it is well known that for a good approximation for ![]() in the gravitational field is given by Moller (1952) and Anderson (1967) as:
in the gravitational field is given by Moller (1952) and Anderson (1967) as:
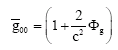 | (18) |
where, Φg is the corresponding universal gravitational potential.
It is well known that the velocity U(η, ξ, φ), the frequency v(η, ξ, φ) and the wavelength λ(η, ξ, φ) of a particle is related by:
| (19) |
where:
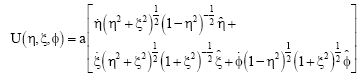
and hence, it follows that the length of space of a photon from a rain drop in the gravitational field exterior to a stationary homogeneous prolate spheroidal massive body is given:
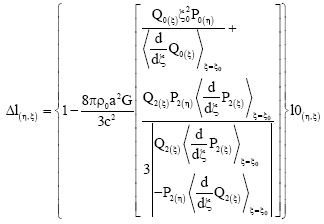 | (20) |
where, Φg, Q0(ξ) and Q2(ξ) are given in Musongong et al. (2004) and λ0(η,ξ)is the proper wavelength. Equation 20 shows that the length of a drop of rain in space is reduced and this equation can be compared to that of perfectly spherical body given by:
| (21) |
APPLICATIONS
Next, we then applied our results to investigate the state of the universe since the universe is oblate spheroidal or prolate spheroidal in shape and the subject rain drop concerns the latter. Many authors have advocated the cosmological red shift as a tired-light mechanism and non-velocity red shift mechanism rather than the gravitational shift (Wesley, 1996). The modelling of the entire universe as a four dimensional manifold, a space-time whose geometry is determined by the matter distribution throughout has the following assumptions:
| • | Directions in space-time are equivalent to conform to the picture of the actual universe uniformly filled with nearly constant matter (isotropy). |
| • | The universe should present the same aspect to all observers, situated in any region of space-time. |
| • | Homogeniety of the universe (constant density). |
For a steady state, the universe is stable wherever it exists. Hence a nontrivial solution of Eq. 21 exists such that Δl = 0 and the first term in Eq. 21 has no contribution as the derivative is taken at ξ = ξ0. We evaluated the harmonics (King-Hele, 1972) involved in Eq. 21 while allowing the radius of the rain drop to vary in the motion of the direction to the plane. Hence Eq. 21 shows that the bifurcation values that are points that demarcate the abrupt change in the structure of the universe. The universe therefore becomes stable under Eq. 21 acknowledging the fact that the universe is not expanding since matter is located in the universe not on the universe.
CONCLUSION
We have developed the length contraction expression for a rain drop the transverse spatial coordinates in space in the field of a stationary homogeneous prolate spheroidal massive body Eq. 21. We have also applied the length contraction expression to arrive at the conclusion that the universe although prolate spheroidal in shape does not contract nor expands. It worth adopting the results of our theoretical research showing that the universe is stationary and it is bodies that move in the gravitational field of the universe that suffer contraction and Cosmology is a result of gravitational defects.








