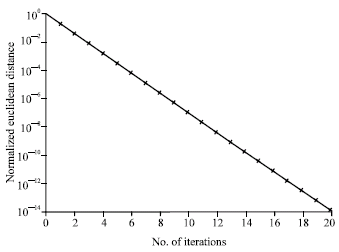
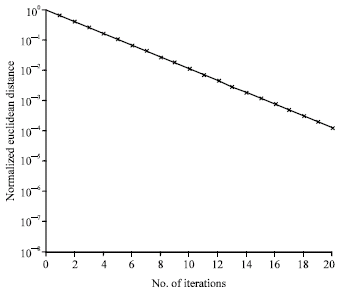
Research Article
On the Performance of Distributed Power Control Algorithm over Wireless CDMA
Faculty of Engineering and Technology, Multimedia University,Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia
C.S. Fong
Faculty of Engineering and Technology, Multimedia University,Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia
A.L. Lock Yen
Faculty of Engineering and Technology, Multimedia University,Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia