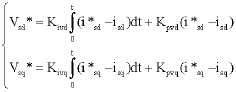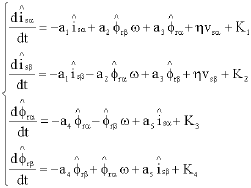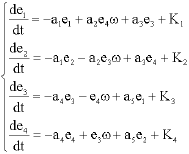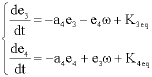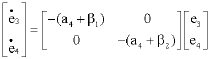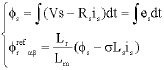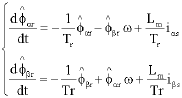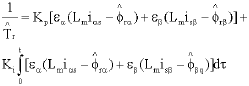Research Article
Adaptative Variable Structure Control for an Online Tuning Direct Vector Controlled Induction Motor Drives
Research Unit of Modeling, Analysis and Control Systems,Department of Electrical and Automatic Engineering, National Engineering School,Gabes 6029, Tunisia
Zaltni Dalila
Research Unit of Modeling, Analysis and Control Systems,Department of Electrical and Automatic Engineering, National Engineering School,Gabes 6029, Tunisia
Abdelkrim Mohamed Naceurq
Research Unit of Modeling, Analysis and Control Systems,Department of Electrical and Automatic Engineering, National Engineering School,Gabes 6029, Tunisia