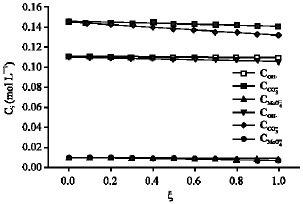
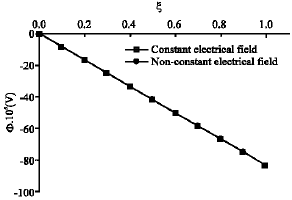
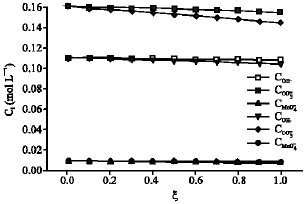
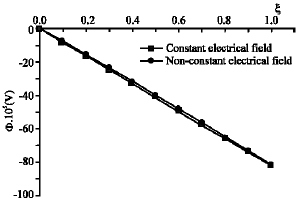
Research Article
Electrotransport of Molybdenum Through an Electrodialysis Membrane. Concentration and Potentiel Profiles in Aqueous Interfacial Layers
Laboratory of Sciences and Material Engineering, Department of Material Sciences, Faculty of Mechanical Engineering and Chemical Engineering, U.S.T.H.B, Algiers, Algeria
Kamel Benmhidi
CDTN Division of Theoretical Physics and Numerical Methods, Algiers, Algeria