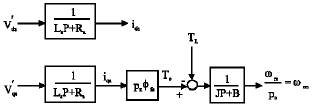
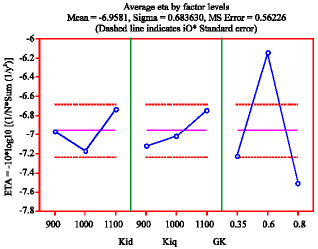
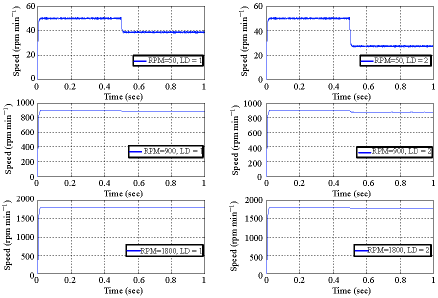
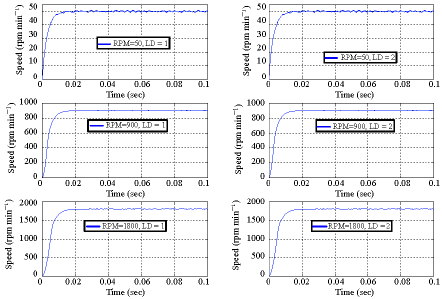
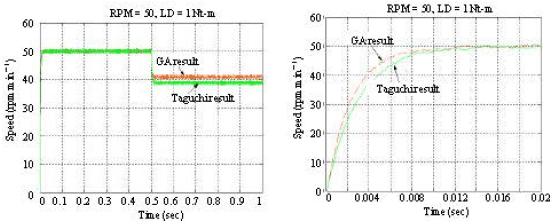
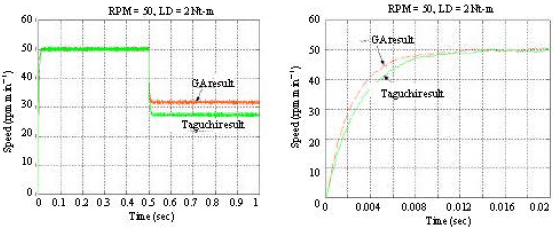
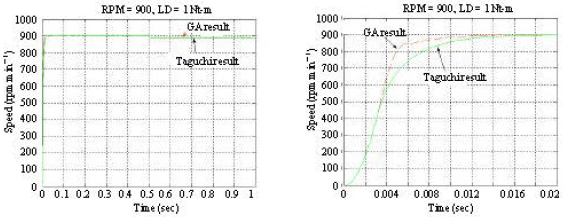
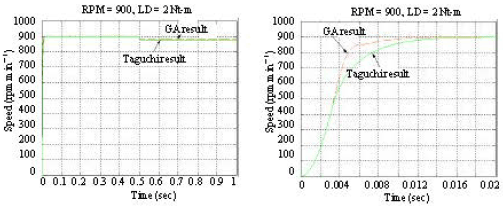
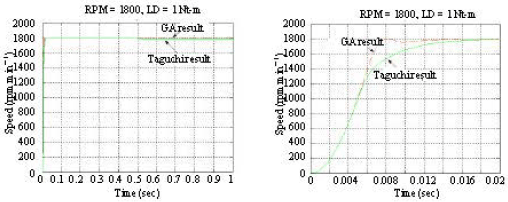
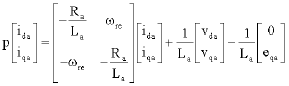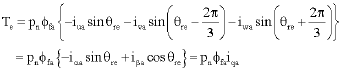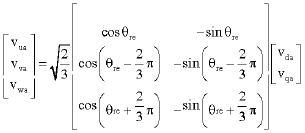Research Article
Optimization of Fuzzy Controller of Permanent Magnet Synchronous Motor
1Department of Refrigeration and Air Conditioning, National Chin-Yi University of Technology, 411 Taiwan, Republic of China
Shou-Ping Hsu
1Department of Refrigeration and Air Conditioning, National Chin-Yi University of Technology, 411 Taiwan, Republic of China
Yung-Hsiang Hung
Department of Industrial Engineering and Management, National Chin-Yi University of Technology, 411 Taiwan, Republic of China