Research Article
Study on Fuzzy Comprehensive Evaluation Approach for Safety Management in Mining Engineering
Department of Environmental Engineering, Zhejiang Gongshang University, Hangzhou 310035, China
The coupling between gas flow and solid deformation in porous media has received a considerable attention because of its importance in the area of multi-physical-fields analysis, contaminant transport and safety management during coal mining (Zhao et al., 1994a, b, 2004; Zhao and Valliappan, 1995; Valliappan and Zhang, 1996, 1999; Wu et al., 1998; Ville, 1998; Sun and Xian, 1998, 1999; Sun, 2002, 2005; Sun and Wan, 2004). Safety management of coal mine is a complex system because coal mine mining engineering is complicated and volatile (Sun and Yu, 1988; Sun, 1990, 1991; Sun and Xian, 1998; Young, 1998; Valliappan and Zhang, 1999; Sun, 2002, 2005; Saghafi et al., 2006 ). It will help to enhance safety management of enterprise and raise coal mine safety management level if safety management level can be evaluated by all kinds of industrial accident, i.e., based on the evaluation, we can determine which mine is best managed and which one is worst, at the same time, find out the degree between the best and worst. The evaluation also can provide basis data for management department to examine management level and award the best one.
In present, the death rate was introduced generally to evaluate the level of coal mine safety management. But such single indicator can’t have comprehension assessment on the safety management level. It is difficult to reflect safety management levels when apply to a small scale coal mine in the south of China because of low coal production and complex safety condition. It is hard to evaluate and arrange on level in proportion. Sometimes the real condition of coal mine safety management can not be reflected even. Generally speaking, the uncertainty is always existed in the judgment on the coal mine safety management, i.e., there is no clearly boundary between best and worst on management level. Because of reasons mentioned above accurate evaluation for safety management of coal mines is difficult. Hence, this article aimed at proposed a new evaluation approach which is focused on the fuzzy mathematics theory for coal mine safety management.
CONSTRUCTION OF MEMBERSHIP FUNCTION
The safety index choosing: The accident is not only the index of mine safety but also an important reflection of the level of mine safety management. Conventionally, the accident whether happened, accident rate, the nature and seriousness of accident are the main factors for evaluation. Generally speaking, the accident rate will decrease if the safety precautions is perfection and the safety rules are sound as well as what is more safety rules should be executed with absolute strictness. Evidently, the accident happened whether or not is corresponding with the level of safety management and so accident rate is a function of safety management. In this study, four indicators (i.e., death rate per million tons, seriously wounded rate per thousand persons, slightly wounded rate per thousand persons and rest days per person) were chosen for evaluation. Certainly, other safety indicators also can be considered such as electromechanical facility accident or accident economic losses etc. But here coal mine safety management comprehensive evaluation approach was introduced only considering the accident rate.
Introduction to fuzzy comprehensive evaluation approach:
So called fuzzy comprehensive evaluation approach is the process that mine safety indicator set (y) converted to fuzzy evaluation factor set (U) by membership function. Then, a fuzzy comprehensive evaluation was completed on the evaluation space S = (X, U, R) and then the result of evaluation index vector B was determined. The component values of index vector B can be used to evaluate the level of mine safety management focus on degree and classification.
In the evaluation space S= (X, U, R), supposed that X = {x1, x2 ● ● ●, xn} is the evaluation objects set; U = {u1, u2, ● ● ●, um} is the fuzzy evaluation factor set; R is fuzzy evaluation matrix which is fuzzy relationship from X to U. The elements of R were determined by the membership function of R: μR (u, x). μR (ui, xi) corresponds to the related elements while (ui, xj)(i = 1,2, ● ● ●, m; j = 1, 2, ● ● ●, n) are given, i.e.,
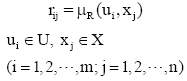 | (1) |
Formula 1 shows that relationship rij is the reflection of factor ui reflecting from mine xj (0 ≤rij≤1) and rij is defined as the membership degree of binary fuzzy sets R at points (ui, xj).
| (2) |
Where, ![]()
ai is weight value of safety index ui. From formula 2 the different importance degree distribution of all safety indexes can be seen and such distribution is the key to fuzzy comprehensive evaluation model. However the methods adopted for determination of weight matrix A in previous literature were determined by both expert appraisals and weight value deciding subjectively, obviously, such method can’t reflect the problem of weight interval distributing of the evaluation factors objectively. Hence, the problem mentioned above is discussed in this article and a new computational approach for weight matrix is proposed.
According to the fuzzy relationship composition, a fuzzy comprehensive evaluation model can be obtained, i.e:
| (3) |
Where, ![]()
the weighted average is adopted for calculation of fuzzy relationship composition; Ordinary logical real number square method is used for multiplication; addition ⊕ is defined as:
| (4) |
Fuzzy set B is the evaluation result, each element bi of B is corresponded to an evaluated mine. The level of all mine’s safety management can be determined according to the value of elements
| (5) |
Where, components of B converted to 0≤bj*≤100, j = 1, 2, ● ● ●, n). According to the formulas above combined with the rules of comprehensive evaluation, evaluation result sets of mine safety management levels can be classified into five groups:
| I | : | mine safety management is the best [90, 100]; |
| II | : | mine safety management is better [80, 90]; |
| III | : | mine safety management is general [70, 80]; |
| IV | : | mine safety management is poor [60, 70]; |
| V | : | mine safety management is worse [0, 60]. |
The meaning and construct of membership function: Construct the membership function by accident rate i.e., membership function will be constructed according to four indicators include death rate per million tons, seriously wounded rate per thousand persons, slightly wounded rate per thousand persons and rest days per person. Combined with the classification interval, the construction and the meaning also can be shown as following.
| • | The planning death rate per million tons in evaluation times is setting at 100 and the lower the better. Assuming Xaj is the percentage of real death rate to planning death rate in mine j, so: |
| Table 1: | Four functions for accident rate of coal mines |
 | |
 |
| • | The planning seriously wounded rate per thousand persons in evaluation times is setting at 100 and the lower the better. xbj is the percentage of real seriously wounded rate to planning seriously wounded rate in mine j, so: |
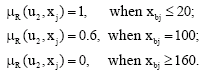
| • | The planning slightly wounded rate per thousand persons in evaluation times is setting at 100 and the lower the better. xcj is the percentage of real slightly wounded rate to planning slightly wounded rate in mine j, so: |
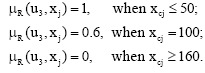
| • | The planning rest days per person in evaluation times is setting at 100 and real rest days is supposed the lower the better. xdj is the percentage of real rest days to planning rest days in mine j, so: |
![]()
According to four conditions of accident rate mentioned above and the conditions given by these four evaluation factors, membership function can be deduced as shown in Table 1.
CALCULATION APPROACH FORWEIGHT MATRIX
We propose a new calculation approach for weight matrix as below.
| • | Setting up a comparison matrix. It is assumed that U = {u1, u2, ● ● ●, um} is a factor set. Each pair of elements ui and uj in U are chosen for comparing by experts according to the evaluation criterion and uİ≠uj. Comparison matrix C = (Cij)mχm can be formed after the results of comparison are indicated. |
The evaluation criterion is shown below.
If ui is one as important as uj, i.e., there is no difference for contribution between ui and uj, Cij= 1 or Cji = 1;
If ui is a little more important than uj, i.e., the contribution of ui is a little more than uj but not obviously, Cij = 2;
If ui is more important than uj, i.e., the contribution of ui is more than uj, but not outstanding, Cij = 3;
If ui is much more important than uj, i.e., the contribution of ui is much more than uj, but a little outstanding, Cij = 4;
If ui is absolutely more important than uj, i.e., the contribution of ui is quite more than uj, Cij = 5;
If importance degree obtained from comparison between ui and uj is the value between two levels, an average value can be token (e.g., 5/2, 7/2, 9/2 etc.).
If ui is not only more important than uj bus also have done great contribution, cij can equal to 5 but can not exceed 5.
Moreover Cij = 1/ Cji. After the comparison between the elements each, a comparison matrix C is formed.
| • | The comparison matrix which is constructed according the comparatively importance of each factors consist of the natures as below: |
Cij>0,
Cij ’ Cji =1, i ≠j; i, j = 1, 2, , ● ● ● ●, m;
Cii =1, i=1, 2,, ● ● ● ●, m.
| • | Determine the largest eigenvalue λmax and corresponding eigenvector W. Weight matrix A can be obtained after standardization of eigenvector. For simplification, an approximate calculation approach is employed as following. |
| • | Each row of comparison matrix C should be standardized; All component of the comparison matrix C are added on column after the standardization; Vector (one row, m column) after aggregation should be standardize again and then the result matrix (We) which is the weight matrix (A ) we want can be obtained; Calculate the largest eigenvalue λmax of comparison matrix C. |
| (6) |
| • | The consistency indicator for verifying the consistency of comparison matrix C should be determined. |
| (7) |
The smaller the η value, the higher consistency degree for the comparison matrix C; Comparison matrix can be considered satisfactory while η<0.1. Therefore the comparison matrix C should be adjusted unless η<0.1.
CASE STUDY OF FUZZY COMPREHENSIVE EVALUATION APPROACH
Case study of fuzzy comprehensive evaluation approach was based on one year’s four indicators of mine safety management for Changguang Coal Mine Corp. Ltd. of Zhejiang province, China. The objection achieved rate of the enterprise was shown in Table 2 and try to comprehensive evaluate the level of mine safety management. The level of mine safety management was classificated according to the evaluation results when evaluation results were determined. Fuzzy evaluation matrix R can be determined according to Table 1 and 2.
Fuzzy weight matrix (A) was determined by next step. In hypothesis, evaluation factor set U = (u1, u2, u3, u4) = (death rate per million tons, seriously wounded rate per thousand peoples, slightly wounded rate per thousand persons, rest days per person). Comparison matrix C can be determined based on evaluation criterion and these four evaluation factors which were focused on reflecting the importance of mine safety management level as Table 3.
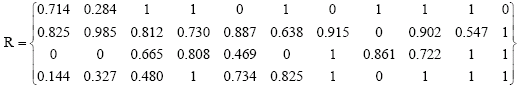 | (8) |
| Table 2: | Four indicators of mine safety management for Changguang Coal Mine Corp. Ltd |
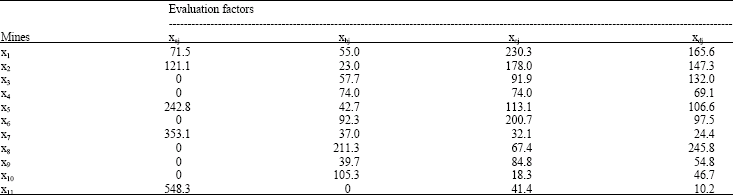 | |
| Table 3: | Matrix C |
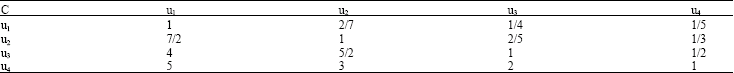 | |
| Table 4: | Evaluation result of mine safety management |
 | |
Then, the result can be calculated as bellows:
| (9) |
| (10) |
| (11) |
Realized from the consistence indicator η, the comparison matrix C constructed is satisfied. Moreover, weight matrix A of four factors corresponds to situation. Then we have:
| (12) |
Matrix A can be determined according to fuzzy relationship composition model (3) and R in the example:
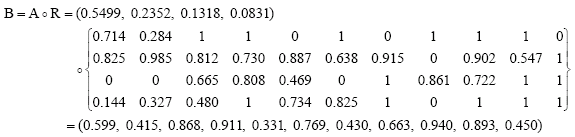
So, B* = The results of fuzzy comprehensive evaluation approach of mine safety management were list in Table 4.
| • | The advantages of fuzzy mathematical theory in application to comprehensive evaluation on mine safety management level includes: Considering problem holistically, the opportunities of subjective and one-sided are reduce and be conventional in quantitative analysis. The fuzzy mathematical theory can avoid the situation that personal feelings may color evaluation. The level of enterprise safety management can be raised when scientific and democratic methods are employed for evaluation and management. |
| • | The result for case study of fuzzy comprehensive evaluation approach showed that the weight distribution determined by this weight matrix calculation approach was reasonable and the classification degree for the level of mine safety management was consistent with the real situation of coal mines. |
| • | Combined with numerical simulation technique, fuzzy comprehensive evaluation approach can be used to handle with complicated matters and large scale computational mathematic models and enterprise safety management can be automation. |