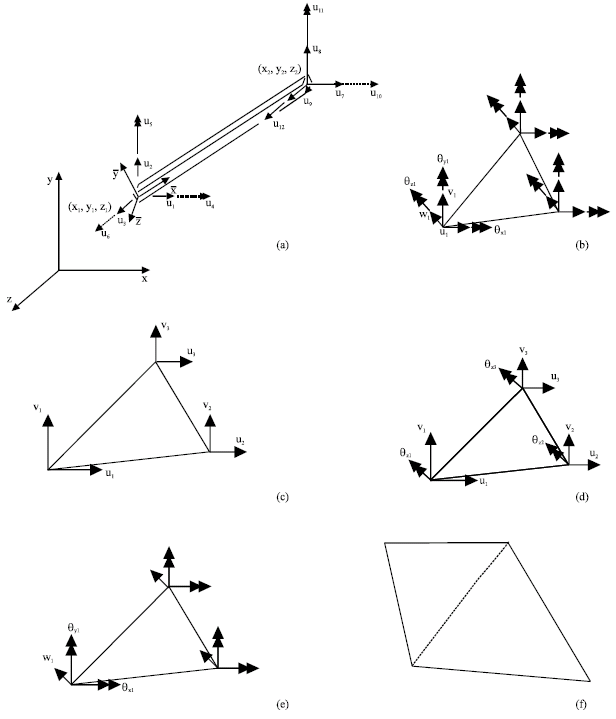
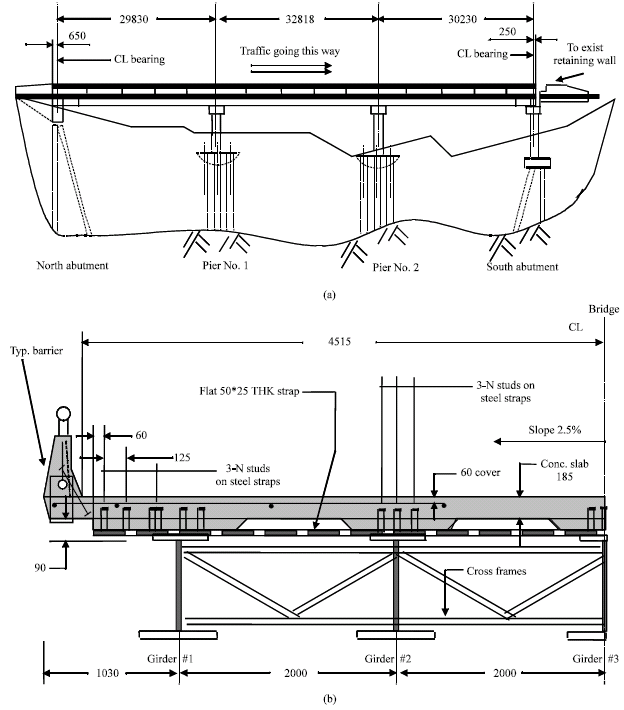
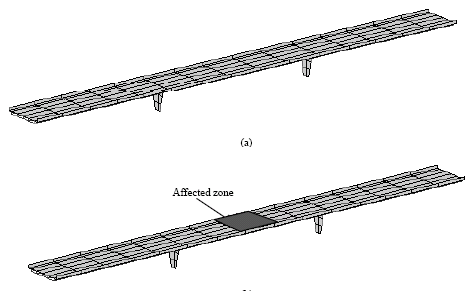
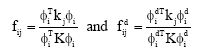Research Article
Development of a Finite Element System for Vibration Based Damage Development of a Finite Element System for Vibration Based Damage Identification in Structures
Department of Building, Civil and Environmental Engineering, Concordia University, Montreal, Canada
Jag Humar
Department of Civil and Environmental Engineering, Carleton University, Ottawa, Canada
Ahmed Noman
Department of Building, Civil and Environmental Engineering, Concordia University, Montreal, Canada