ABSTRACT
Anomalies observed on gravity maps of sedimentary basins are the integrated effects of faults, folds and intrusive bodies of basement or intra sedimentary origin. By computing a 2-D Cross Correlation Function (CCF) between the gravity data and the gravity anomaly due to a step structure, normal and reverse faults can be mapped from elongated contours of maxima and minima in the CCF map. The method was employed to map faults in part of the Benue trough, Nigeria. Some of the faults identified correlate well with known faults shown on the regional structural map of Nigeria. Although the status of the unconfirmed faults can only be ascertained through field investigations, the dominant N-S, NE-SW and E-W strike directions fit into the general pattern of strike slip tectonic features and mineralized zones associated with the trough.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2007.226.231
URL: https://scialert.net/abstract/?doi=jas.2007.226.231
INTRODUCTION
Mapping faults within a sedimentary basin is critical to an exploration program for oil, gas, petroleum, groundwater and solid minerals. Even where the basement is highly fractured, the overlying sediments hide them from view. However, these fractures are reactivated at later times during, or after, deposition of the sedimentary section and create structures and/or sedimentary facies that become oil and gas traps and reservoirs.
Pierce et al. (1998) showed that fluid flow along vertically aligned fractures is an important factor controlling the deposition of minerals in sedimentary sections. The working hypothesis is that fluids scavenge metals from the basement rocks and these fluids move regionally up-dip along fractures of opportunity. When the metals-rich fluid reach a reducing environment such as shale or a hydrocarbon charged zone, a variety of iron rich minerals are precipitated. Similarly, groundwater movement and accumulation in rocks is facilitated by the increased secondary porosity and permeability resulting from a network of fractures and faults.
On potential field maps, fractures and faults mark zones where there are changes in the density or magnetic susceptibility of the rock mass. In particular, gravity data in sedimentary basins are sensitive to vertical offsets across high-angle faults, where rocks with different densities are juxtaposed. Therefore, faults can be identified on gravity anomaly maps using any of the available schemes for mapping contacts such as the calculation of derived fields: The horizontal gradient magnitude, the analytic signal and the local wavenumber or their enhanced equivalents, such as the enhanced analytic signal amplitude and the enhanced local wavenumber.
The method used to map faults in this study was described by Zeng et al (1994). It is based on the calculation of the Cross Correlation Function (CCF) between the gravity anomaly of an area and the gravity anomaly due to a model fault. The main restriction here is that the displacement on the fault is vertical as in normal or reverse faults so that the structure can be represented by a step.
THEORY OF THE METHOD
Let go(n), n = 1, 2, 1………M, represent the observed Bouguer anomaly values at M points along a profile and gf(n'), n' = -N,Y,0,YYN are the calculated anomalies along a profile perpendicular to the strike of a step fault. Since we are interested in shallow faults, the observed and the calculated gravity values may be replaced by their second vertical derivative functions go” (n) and gf” (n), respectively. Then, the Cross Correlation Function (CCF) between go”(n) and gf”(n’) at point x on the profile is given by:
| (1) |
Where x = N+1, N+2,………………,M - N. The discrete form of the second vertical derivative of the gravity anomaly due to a step is given by
| (2) |
where I = -N, …,-1,0,1,2,……N, Δx is the station spacing, G is the gravitational constant, ρ is the density contrast of the step, h1 and h2 are the depths to the top and bottom of the step, respectively.
Since the gravity anomaly go(n) includes the effects of faults that may exit in the area, then the moving window CCF expressed in Eq. 1 produces a maximum at each point x along the profile where there is a fault. The CCF method has an additional advantage which is not provided by the application of derived fields mentioned earlier. This relates to the polarity of the fault with respect to the location of the downthrown/upthrown side of the step. Where the polarity of the detected faults is the same as that of the model step, the CCF is a maximum. If the polarity of the fault is opposite that of the model step, the CCF is a minimum. Furthermore, because the faults will generally have different strike directions, it is necessary to perform the cross correlation analysis along two orthogonal directions, namely along profiles in the east-west and north-south directions of the grid in order to map all faults. Consequently, two maps of the CCF are required for fault mapping in a given area.
The study area: The study was conducted on a 12, 100 km2 area bounded by latitudes 7°30' and 8°30' and longitudes 8°30' and 9°30' and located in the Benue trough, Nigeria. The northeast trending trough is about 800 km long and 80 to 150 km wide and is filled with Cretaceous rocks whose age range from middle Albian to Maastrichtian. It is bounded on either side by granite and gneisses of probably Palaeozoic age, which make up the crystalline basement. Structures in the area include two major anticlines, the Keana anticline, which trends some 64 km in a north-easterly direction from east of Keana and another which runs with ENE trending axis immediately north of Awe Cratchley and Jones (1965). Faulting is significant in the area and the en echelon arrangement of some of the folds axes suggest sinistral movement along NNE shear faults (Benkhelil, 1982).
PROCESSING AND ANALYSIS OF GRAVITY DATA
The gravity data used in this study was taken from the Bouguer anomaly map of the Benue valley (Fig. 1) prepared by Cratchley and Jones (1965). The contour map was digitized and interpolated unto a square grid with a spacing of 1.0 km. A contour map of the gravity field is shown in Fig. 2a. The major trend of the contours is southwest-northeast, parallel to the trend of the trough. In the central and southeastern portions, the trend of the contours is mainly east-west. The magnitude of the gravity field increases from the northwestern corner to the east and to the south. A prominent closure of gravity low occurs near the center of the study area.
Since we are interested in shallow faults, a Second Vertical Derivative (SVD) map was produced to highlight the short wavelength anomalies and suppress the long wavelength anomalies associated with deep structures. This was achieved using the FFT technique, thus necessitating that the grid be preconditioned by detrending and tilting to make the southeast and northwest corners equal.
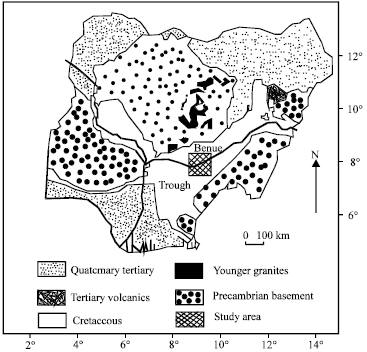 | |
| Fig. 1: | Generalized geological map of Nigeria showing the Benue trough and the study area |
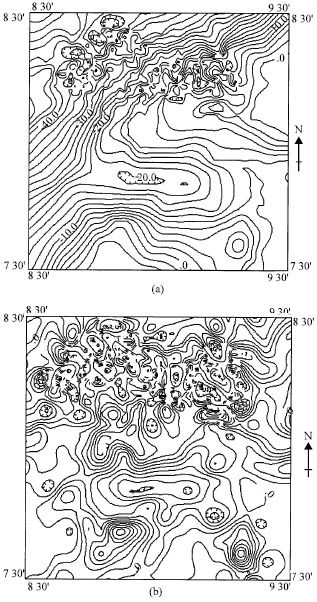 | |
| Fig. 2: | (a) Bouguer anomaly map of the study area and its (b) second vertical derivative field |
This was followed by extrapolating the data in the north and east directions using a cosine taper to make the opposite sides of the data wrap smoothly in both directions. This pre-conditioning significantly minimizes the distortion of the high frequency and axial regions of the spectra, characteristic of the discrete transform (Cordell and Grauch, 1982). Furthermore, because of the amplification of noise in second derivative computation, the SVD data was subjected to a low-pass filter to suppress the high frequency noise components. The resulting SVD map is shown in Fig. 2b.
RESULTS AND DISCUSSION
The CCF maps for the east-west and north-south directions are shown in Fig. 3.
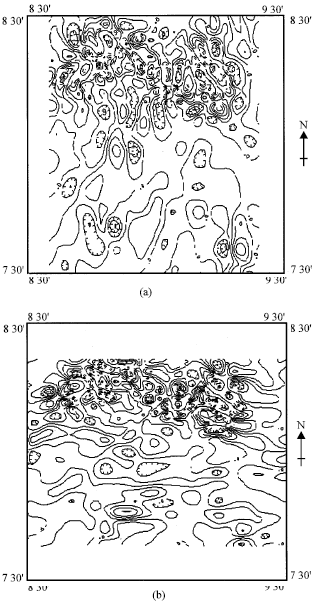 | |
| Fig. 3: | Maps showing the normalised cross correlation functions for (a) east-west and (b) north-south directions |
Faults can be interpreted on these maps by drawing lines along the long axis of elongated closures defining maxima or minima in the contour pattern as described by Zeng et al (1992). A different and less subjective approach was used to mark out maxima and minima in this study. This involved the use of the computer program BOUNDARY described by Phillips (1992), which automatically identifies points of maxima on the CCF grid. In order to use the same program to identify points of minima, the values on the CCF grid were multiplied by -1 before the search for maxima which actually are minima. In effect, two maps showing maxima (Fig. 4) and minima (Fig. 5), respectively were produced for each CCF map. On these maps, a fault will be taken to consist of points which are contiguous and display unambiguous continuity.
 | |
| Fig. 4: | Maps showing the maxima of the cross correlation functions for (a) east-west and (b) north-south directions |
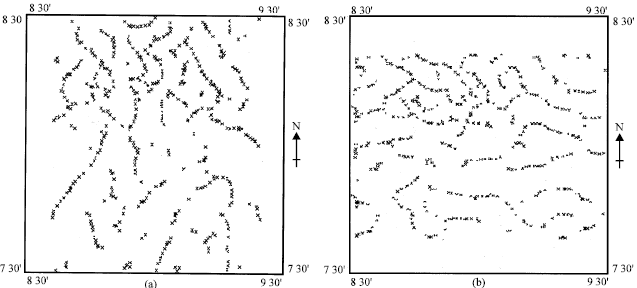 | |
| Fig. 5: | Maps showing the minima of the cross correlation functions for (a) east-west and (b) north-south directions |
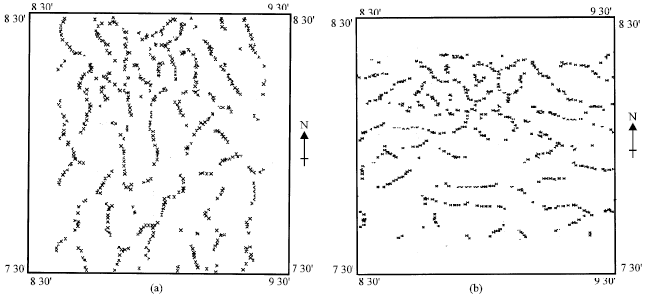
Based on this criterion, faults interpreted from the maxima and minima of the CCF for the study area are shown in Fig. 6 and 7, respectively.
At present, there is no field data to corroborate the mapped faults. However, one can rely on both direct and indirect evidence. The former derives from the regional structural map of Nigeria prepared by the Geological Survey, Nigeria (1985). Some of the faults interpreted from the CCF maps coincide with fractures on the structural map particularly when the short aligned segments in the former are joined together to form continuous and longer features (Fig. 8). Indirect evidence of these faults is sourced from the occurrence of lead-zinc mineralization in the area. These are restricted to Albian and Cenomanian strata and are better defined on lobes located in steeply-dipping fracture-filled veins striking mainly north-south and grouped in NE-SW zones generally associated with the axes of the major anticlines (Cratchley and Jones, 1965). Some of the north-south trending faults are normal faults resulting from the major strike-slip movements associated with the formation of the trough (Benkhelil).
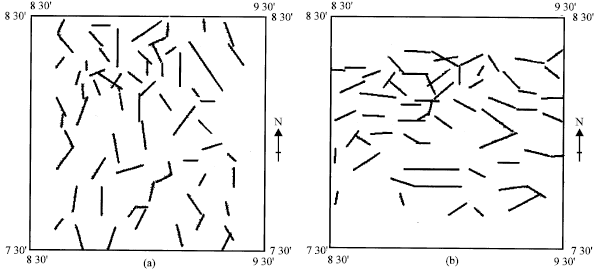 | |
| Fig. 6: | Maps showing the faults deduced from the maxima of the cross correlation functions for (a) east-west and (b) north-south directions |
 | |
| Fig. 7: | Maps showing the faults deduced from the minima of the cross correlation functions for (a) east-west and (b) north-south directions |
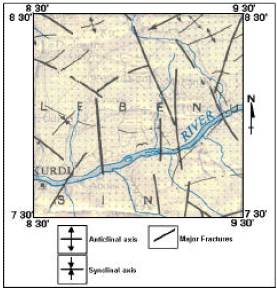 | |
| Fig. 8: | Structural map of the study area showing major fractures and folds (after Geological Survey of Nigeria, 1985) |
CONCLUSIONS
The anomalies observed on a typical Bouguer anomaly map represent the integrated effects of lateral variations in rock density due to faults, intrusive bodies, shear zones, etc. Faults of the normal or reverse type can be identified easily on gravity anomaly profiles. Using the same method to identify faults on maps can be tedious and time consuming particularly for large areas. However, the use of the cross correlation function technique, as demonstrated in this study, is efficient and rapid. When data on a gravity anomaly map is correlated with the gravity effect of a model step, maximum positive correlation occurs at points where the observed anomaly has the same polarity as that of the model fault while a minimum occurs where they have opposite polarities. Application of the method to part of the Benue trough, Nigeria facilitated the identification of known faults and others which have not been mapped previously.








