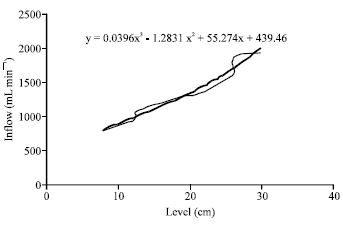
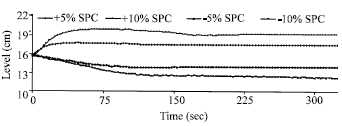
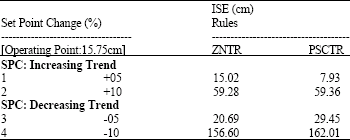
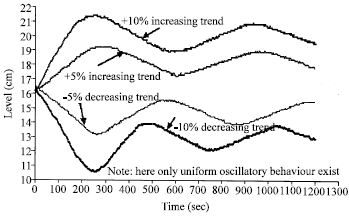
Research Article
Real Time Implementation of Wiener Model PI (WMPI) Controller in a Conical Tank Liquid Level Process
Department of Chemical Engineering, Faculty of Engineering and Technology, Annamalai University, Annamalainagar-608 002, Tamil Nadu, India
S. Sathishbabu
Department of Instrumentation Engineering, Faculty of Engineering and Technology, Annamalai University, Annamalainagar-608 002, Tamil Nadu, India
A. Asokan
Department of Instrumentation Engineering, Faculty of Engineering and Technology, Annamalai University, Annamalainagar-608 002, Tamil Nadu, India
T. Karunanithi
Department of Chemical Engineering, Faculty of Engineering and Technology, Annamalai University, Annamalainagar-608 002, Tamil Nadu, India