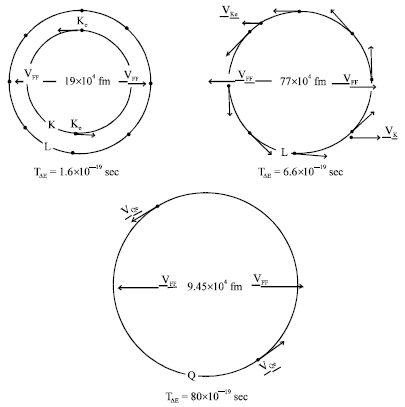
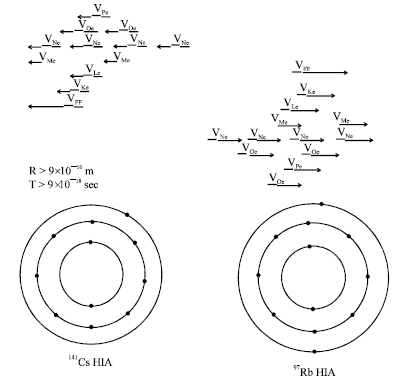
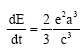Research Article
Atom Behavior During Nucleus Fission Process (Highly Ionized Atoms (HIA) Hypothesis)
Department of Applied Physics, Tafila Technical University, Tama, Jordan
A.A. Mahasneh
Department of Applied Physics, Tafila Technical University, Tama, Jordan