Research Article
Short Term Load Forecasting Using Artificial Neural Networks for the West of Iran
Department of Electrical Engineering, Faculty of Engineering, Razi University, Tagh-e-Bostan, Kermanshah-67149, Iran
Neural networks have seen an explosion of interest over the last few years and are being successfully applied across an extraordinary range of problem domains, in areas as diverse as finance medicine, engineering, geology and physics. Indeed, anywhere that there are problems of prediction, classification or control, neural networks are being introduced. Neural networks could be defined as an interconnection of simple processing elements whose functionality is based on the biological neuron. Biological neuron is a unique piece of equipment that carries information or a bit of knowledge and transfers it to other neurons in a chain of networks. Artificial neuron imitates these functions and their unique process of learning. However, Artificial Neural Network (ANN) has been replacing traditional methods in many applications offering, besides a better performance, a number of advantages: no need for system model, bizarre tolerance patterns, notable adaptive capability and so on. Load forecasting is one of the most successful applications of ANN in power systems. Short Term Load Forecasting (STLF) refers to forecasts of electricity demand (or load), on an hourly basis, from one to several days ahead (Mandal et al., 2006; Topalli et al., 2006; Kandil et al., 2006; Huang and Shih, 2003). The short term load forecasting (one to twenty four days) is of importance in the daily operations of a power utility. With the emergence of load management strategies, the short term load forecasting has played a greater role in utility operations. The development of an accurate, fast and robust short-term load forecasting methodology is of importance to both the electric utility and its customers. Many algorithms have been proposed in the last few decades for performing accurate load forecasting. The most commonly used techniques include statistically based techniques like time series, regression techniques and box-jenkis models (Moghram and Rahman, 1989) expert system approaches (Rahman and Bhatnager, 1988) and ANNs (Mandal et al., 2006; Topalli et al., 2006; Kandil et al., 2006; Huang and Shih, 2003; Senjyu et al., 2002; Taylor and Buizza, 2002). The objectives of this study are:
| • | To use three important architectures of neural networks i.e., MLP, ERNN and RBFN methods for short term load forecasting. |
| • | To compare the performance of three methods. |
| • | To find minimum forecasting error as compared to other result (Mandal et al., 2006). |
| • | Finally to find the best method to model the STLF system. |
For developing the forecasting models, we used the actual hourly electrical load data provided by the west electric company, Iran for the years 2005 through 2006 for the west of Iran. The weather variables such as temperature, humidity, wind speed, sky condition (cloud cover) and sunset (day light time) affect the forecasting accuracy and are included, also season (month) and day of the week are included in the model too.
Load demand pattern: A broad spectrum of factors affects the system’s load level such as trend effects, cyclic-time effects, weather effects, random effects like human activities, load management and thunderstorms. Thus the load profile is dynamic in nature with temporal, seasonal and annual variations.
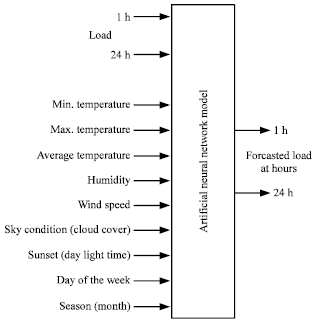 | |
| Fig. 1: | Input-output schematic of system |
In this study, we develop a system as shown in Fig. 1 with inputs parameters such as past 24 h load, temperature, humidity, wind speed, sky condition (cloud cover), sunset (daylight time), season (month) and day of the week to forecast 24 ahead load demands (output) for the west of Iran using artificial neural networks.
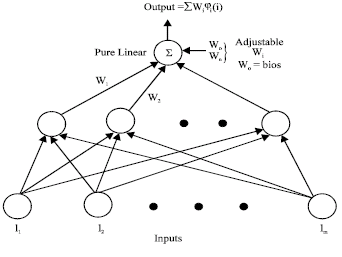
Computational intelligence models: The three models of neural networks are selected among the main network architectures used in engineering. The basis of all models is neuron structure. These neurons act like parallel processing units as shown in Fig. 2, where X1, ..., XN are inputs and W1, ..., WN are input weights.
Multi Layer Perceptron (MLP): This is perhaps the most popular network architecture in use today. Its units each perform a biased weighted sum of their inputs and pass this activation level through a transfer function to produce their output and the units are arranged in a layered feed forward topology. The network thus has a simple interpretation as a form of input-output model, with the weights and thresholds (biases) the free parameters of the model. Such networks can model functions of almost arbitrary complexity with the number of layers and the number of units in each layer, determining the function complexity. Important issues in Multilayer Perceptron design include specification of the number of hidden layers and the number of units in these layers (Bishop, 1995; Haykin, 1994). Once the number of layers and number of units in each layer, has been selected, the network’s weights and thresholds must be set so as to minimize the prediction error made by the network. This is the role of the training algorithms. The best known example of a neural network training algorithm is back propagation (Haykin, 1994; Patterson, 1996). Modern second-order algorithm such as conjugate gradient descent and Levenberg-Marquardt (Bishop, 1995) are substantially faster for many problems, but Back propagation still has advantages in some circumstances and is the easiest algorithm to understand. With this background we designed and trained the network as follows: the three-layer network with Sigmoid transfer function for hidden layer and linear transfer function for output layer has been selected. The MLP structure is shown in Fig. 3.
Back propagation training algorithms are often too slow for practical problems, so we can use several high performance algorithms that can converge from ten to one hundred times faster than back propagation algorithms. These faster algorithms fall into two main categories: heuristic technique (variable learning rate back propagation, resilient back propagation) and numerical optimization techniques (conjugate gradient, quasi-Newton, Levenberg-Marquardt). We tried several of these algorithms to get the best result. Levenberg-Marquardt is the fastest algorithm but as the number of weights and biases in the network increase, the advantage of this algorithm decrease, so we tried another algorithm which perform well on function approximation and converge rather fast. From these algorithms, conjugate gradient was suitable for our purpose. Neural networks generally provide improved performance with the normalized data.
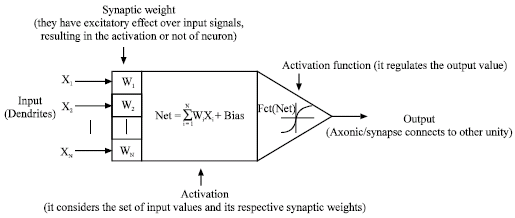 | |
| Fig. 2: | Neuron model and excitation function |
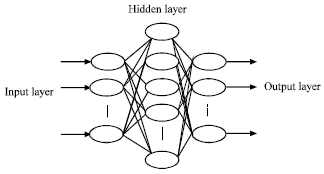 | |
| Fig. 3: | Three layer MLP |
The use of original data as input to neural network may cause a convergence problem. All the data sets were therefore, transformed into values between -1 and 1 through dividing the difference of actual and minimum values by the difference of maximum and minimum values subtracted by 1. At the end of each algorithm, outputs were denormalized into the original data format for achieving the desired result. From one initial condition the algorithm converged to global minimum point, while from another initial condition the algorithm converged to a local minimum so it is better to try several different initial conditions in order to ensure that optimum solution has been obtained (Hagan et al., 1996). Training goal for the networks was set to 10–5. Finding appropriate architecture needs trial and error method. Networks were trained for a fixed number of epochs. By this way, we found that 17 neurons for hidden layer at 500 epochs produce good result. Comparison of 24 h ahead load forecasting with MLP and exact load is shown in Fig. 4a-c.
Elman recurrent networks: Elman networks are just like back propagation networks, with addition of a feedback connection from the output of the hidden layer to its input. This feedback path allows Elman networks to learn to recognize and generate temporal patterns, as well as spatial patterns. This makes Elman networks useful in such areas as signal processing and prediction where time plays a dominant role (Hagan et al., 1996). Because Elman networks are an extension of two-layer Sigmoid/linear architecture (Haykin, 1999; Zurada, 1992), they inherit the ability to fit any input/output function with a finite number of discontinuities. They are also able to fit temporal patterns, but may need many neurons in the recurrent layer to fit a complex function. Also because of the more complex architecture of the recurrent model, there is a significant increase in training time compared with the MLP model. Figure 5 shows an Elman structure, where I1, ..., In are inputs and O1, ..., Om are outputs.
For finding the appropriate architecture of Elman recurrent network, previous steps at MLP designing was followed and found that 11 neurons for hidden layer at 1000 epochs produce good result.
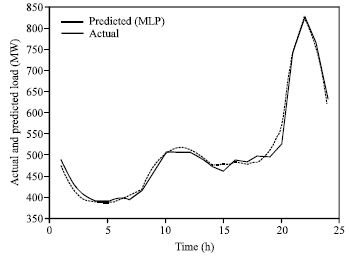 | |
| Fig. 4a: | Comparison of 24 h ahead load forecasting using MLP and exact load for 9-May-2005 |
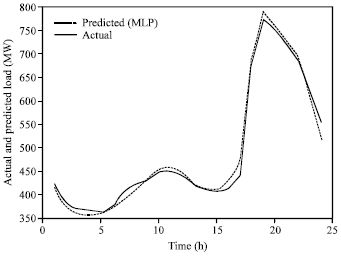 | |
| Fig. 4b: | Comparison of 24 h ahead load forecasting using MLP and exact load for 23-Nov-2005 |
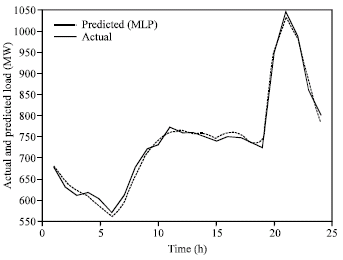 | |
| Fig. 4c: | Comparison of 24 h ahead load forecasting using MLP and exact load for 2-July-2006 |
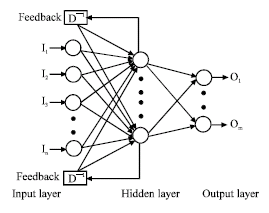 | |
| Fig. 5: | Architecture of Elman recurrent network |
Comparison of 24 h ahead load forecasting with ERNN and exact load is shown in Fig. 6a-c.
Radial Basis Function (RBFN): Radial basis function was then applied to each center. There is one radial Gaussian function for each hidden unit which simulates the effect of overlapping and locally tuned receptive fields. The activation function of hidden nodes is radially symmetric in input space, the magnitudes of activation given a particular record is decreasing function of the distance between the input vector of the record and the center of the basis function. The role of hidden units is to perform a non-linear transformation of the input space A. Radial Basis Function Network is a hybrid learning neural network. It’s a two layer fully-connected network with an input layer which performs no computation. It uses a linear transfer function for the output units and Gaussian function (Radial basis function) for input units (Hagan et al., 1996; Powell, 1992; Zurada, 1992). Learning in the hidden layer is performed by using an unsupervised method, the K-mean algorithm. First, the user must choose a number of centers and this number will correspond to the number of neurons in hidden layer. The K-means algorithm is used to position the centers in the best way, so that each presented record is attached to its nearest center (or cluster). As it is an unsupervised learning method, only the inputs data are presented to K-means algorithm. Learning in the output layer is performed by computing a linear combination of activation of the basis functions, parameterized by weights W between hidden and output layer. Radial basis networks may require more neurons than standard feed-forward Back propagation networks, but often they can be designed in a fraction of the time it take to train standard feed-forward networks. They work best when many training vectors are available. A Generalized Regression Neural Network (GRNN) is often used for function approximation.
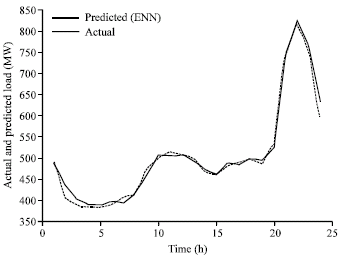 | |
| Fig. 6a: | Comparison of 24 h ahead load forecasting using ERNN and exact load for 9-May-2005 |
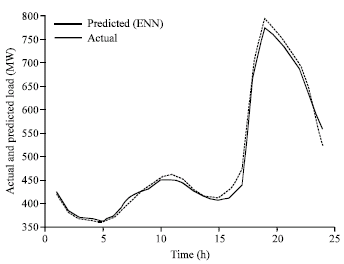 | |
| Fig. 6b: | Comparison of 24 h ahead load forecasting using ERNN and exact load for 23-Nov-2005 |
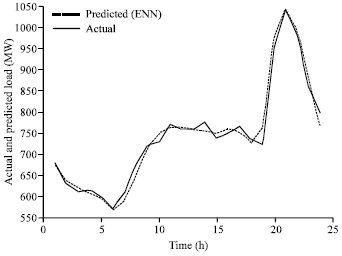 | |
| Fig. 6c: | Comparison of 24 h ahead load forecasting using ERNN and exact load for 2-July-2006 |
 | |
| Fig. 7: | RBFN structure |
 | |
| Fig. 8a: | Comparison of 24 h ahead load forecasting using RBFN and exact load for 9-May-2005 |
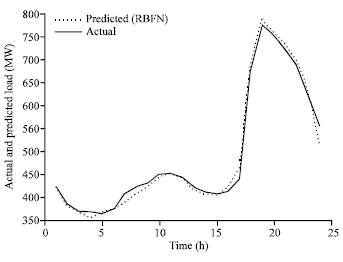 | |
| Fig. 8b: | Comparison of 24 h ahead load forecasting using RBFN and exact load for 23-Nov-2005 |
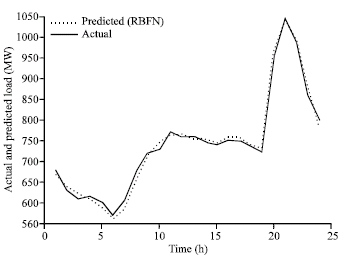 | |
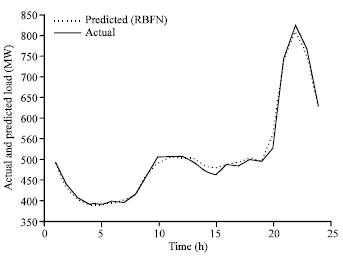
| Fig. 8c: | Comparison of 24 h ahead load forecasting using RBFN and exact load for 2-July-2006 |
It has been shown that, given a sufficient number of hidden neurons, GRNNs can approximate a continuous function to an arbitrary accuracy. Probabilistic Neural Networks (PNN) can be used for classification problems. Their design is straightforward and does not depend on training. These networks generalize well. Figure 7 shows RBFN common structure, where I1, ..., Im are inputs.
Designing a radial basis function network often takes much less time than training a Sigmoid/linear network (Khan and Ondrusek, 2000) in RBFN, neurons increase till error goal or maximum number of neurons reach. The good result obtained with error goal of 10–5 and maximum number of neurons equal to 19. Comparison of 24 h ahead load forecasting with RBFN and exact load is shown in Fig. 8a-c.
The assessment of the prediction performance of the different soft computing models was done by quantifying the prediction obtained on an independent data set. The Mean Absolute Percentage Error (MAPE) were used to study the performance of the trained forecasting models for the testing years. MAPE is defined as follows:
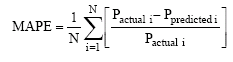 |
Where Pactual I is the actual load on day I and Ppredicted I is the forecast value of the load on that day. Where N represents the total number of data (hours). The Mean Absolute Percentage Error (MAPE) results (Table 1) for three important architectures of neural networks i.e., Multi Layer Perceptron (MLP), Elman Recurrent Neural Network (ERNN) and Radial Basis Function Network (RBFN) and their optimal structures are shown in Table 1.
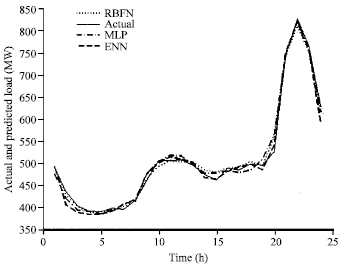 | |
| Fig. 9a: | Comparison of all computational method for 24 h ahead load forecasting and exact load for 9-May-2005 |
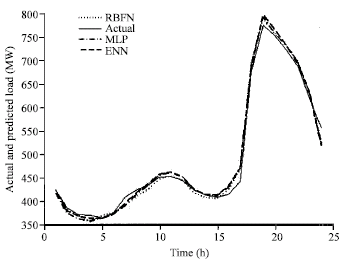 | |
| Fig. 9b: | Comparison of all computational method for 24 h ahead load forecasting and exact load for 23-Nov-2005 |
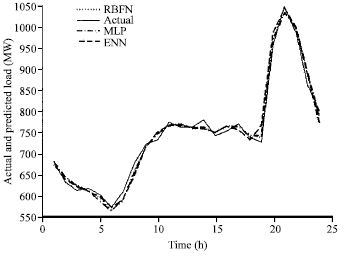 | |
| Fig. 9c: | Comparison of all computational method for 24 h ahead load forecasting and exact load for 2-July-2006 |
| Table 1: | Comparison of optimal structures and MAPE index for three types of neural network |
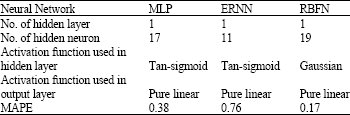 | |
It has been observed that error associated with each method depends on several factors such as the homogeneity in data, the choice of model, the network parameters and finally the type of solution. The learning method for MLP and ERNN were based on back propagation algorithm. As the learning process is time-consuming in back propagation algorithm and there is no exact rule for setting the number of hidden neurons to avoid over fitting or under fitting, therefore, in order to eliminate such problems, the RBFN has been applied. The results obtained clearly demonstrate that RBFN are much faster and more reliable for short term load forecasting. The results obtained as shown in Table 1 shows:
| • | Optimal structures for three types of neural network for obtaining minimum forecasting error. |
| • | Minimum forecasting error is obtained for each method. |
| • | RBFN method has minimum forecasting error (error = 0.17) as compared to ERNN (error = 0.76) and MLP methods (error = 0.38) and even as compare to other result (error = 0.72) (Mandal et al., 2006). |
| • | RBFN due to its minimum forecasting error is the best method in general to model STLF system. |
| • | Finally the results obtained clearly demonstrate that RBFN are much faster and more reliable and accurate and effective for short term load forecasting. |
The comparison of all computational method i.e., MLP, ERNN and RBFN for 24 h ahead load forecasting and exact load for three different days are shown in Fig. 9a-c.
A comparative study of soft computing models for load forecasting shows that RBFN is more accurate and effective as compared to MLP and ERNN. Error associated with each method depends on several factors such as the homogeneity in data, the choice of model, the network parameters and finally the type of solution. ANNs have gained great popularity in time-series prediction because of their simplicity and robustness. The learning method is normally based on the gradient descent method _ back propagation algorithm. Back propagation algorithm has major drawbacks: the learning process is time-consuming and there is no exact rule for setting the number of hidden neurons to avoid over fitting or under fitting and hopefully, making the learning phase convergent. In order to eliminate such problems, the RBFN has been applied. The results obtained clearly demonstrate that RBFN are much faster and more reliable for short term load forecasting.
We would like to express our gratitude to Mr. A. Karimi, the manager of west electric company, Mr. M. Ghasemi, Manager of west of Iran Meteorological Research Center for providing us the required data.