Research Article
Investigation of Sediment Patterns at River Confluence
Department of Hydraulic Structure, Shahid Chamran Umversity, Ahwaz, Iran
M. Shafai Bajestan
Department of Hydraulic Structure, Shahid Chamran Umversity, Ahwaz, Iran
The location where two rivers combined is defined as river channel confluence. Due to three dimensional flow structure at this location, especially due to the downstream mixing of flow, a deep scour hole and a point bar are developed. The scour hole and point bar can cause change in river morphology which accelerate the rate of bank erosion. In river confluence six different zones are distinguished which can be shown as in Fig. 1.
Flow separation at the left river bank just downstream of the river confluence or zone 3, is the main cause for creation of horizontal vortex in this zone. Sediment can accumulate in the center of this zone and create a point bar. As the dimensions of point bar is increased, the flow velocity in the Zone 4, is increased and scour hole dimensions in this zone become larger and larger. Because of this, bank failure will accelerate at the right river bank and a meander is developed. The flow vortex and high flow velocity in this zone can also create problems for navigation. Because of this, the study of flow pattern, scour and sedimentation at river confluence has attracted the attention of many researchers. Due to complexity of the problem because of three dimensional flow and sediment, most of the studies have been conducted experimentally. Mosley (1976) conducted experimental tests for a Y-shape river confluence in a small flume. His results showed that the scour hole increases very fast as river influence angle increases from 15 to 75 degree then the rate of scour hole decreases.
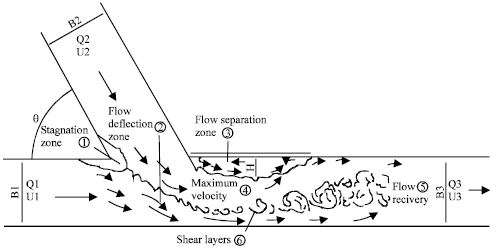 | |
| Fig. 1: | Flow pattern at channel confluence, modified from Best (1987) |
The experimental and field measurement conducted by Ashmore and Parker (1983), for a braided river shows that the confluence angle has the most effective parameters on scour hole dimensions. They developed the following Eq:
| (1) |
In which RDS is the ratio of maximum scour depth to the mean flow depth at the upstream of the channels and θ is the confluence angle in degree.
Best and Reid (1984) conducted experimental studies. Four different confluence angles 15, 45, 70 and 90 degree were studied. They proposed relationships for prediction of flow separation dimensions. They found that the shape index of separation zone which defined as the ration of H/L, in which H and L are width and length of separation zone respectively, are almost constant and equal to 0.19.
Best (1988) conducted experimental and field measurement studies and developed the following equation:
| (2) |
In which θ is the confluence angle in degree. The values of θ in Best experimental tests were selected as 15, 45, 75, 90 and 105 degrees. Roy and Roy (1988) conducted field measurement on 30 river confluences in a watershed basin. They found that in all these locations usually the flow area cross-section downstream of river confluence is decreased and the flow velocity increases. They found that the flow velocity in the scour hole can reach 1.6 times greater than the upstream flow velocity. Biron et al. (1993, 1996, 2002) studied the bed morphology of river confluence of unequal depth. During their study, they found that river bed morphology is changed even the scour hole dimensions remain constant. They found that river morphology in unequal channel depth is different than in a river confluence of equal channel depth. Gurram et al. (1997) also studied the flow pattern in river confluence. Three different angles 30, 60 and 90 degrees were studied. They develop relationships for prediction of flow separation in Zone 3. Their results showed that the shape index of separation zone is almost constant equal to 0.17. Webber et al. (2001) measured the velocity vectors in three dimensions in a 90 degree river confluence. Their measurement showed a vertical variation of separation width in which it is increasing from the channel bed to the water surface. The geometric dimensions of flow separation were related to the ratio of main channel discharge to the lateral channel discharge (Q1/Q2). Measurements of downstream and cross-stream velocities at a small, asymmetrical stream confluence by Rhoads and Kenworthy (1995) show that the structure of low stage flow is influenced by momentum ratio of lateral to main channel, total discharge and bed morphology. Parsons et al. (2007) by measuring 3D flow and bed morphology within a very large confluence-diffluence unit, in Parana river showed that the flow within confluence-diffluence is dominated largely by bed roughness and secondary flow cells that have been identified as important aspect of flow field compare to the smaller channels and assumed to be presented only within large rivers. Boyer et al. (2006) measured the near-bed flow turbulence, bed load transport rates and change in bed morphology during several events within a sand bed discordant confluence. They examined the relations between the flow and sediment transport in confluences. Their measurement showed that heigh sediment transport rates occur at the edges of shear layer region. Sukhodolov and Rhoads (2001) investigated 3D flow structure at three confluences. Their analysis has focused on characteristic of turbulence within the shear layer and in the ambient flow. Result of their experimental test showed that the turbulence kinetic energy within the shear layer is 2-3 times grater than the turbulence kinetic energy of the ambient flow. Borghei and Nazari (2004) also conducted experimental studies in 90 degree river confluence. Their results show that as sediment size, ratio of Q1/Q3 and B2 decreases, the scour depth increases.
Although it seems that the flow pattern and sedimentation of river in confluence have been studied by several investigators, the understanding of the effects of all parameters in formation of scour hole and point bar appears to be incomplete. Most of the studies have focused on the effect of one parameter and other parameters have been kept constant. The river confluence angle is one of the parameters which affect most and only two studies have conducted in the past to investigate its effect. Those studies have not considered the effects of other parameters at the same time. The relations, Eq. 1 and 2, which they have developed is not practical because these equations are not dimensionless and are valid for their experimental results. Therefore it is the main purpose of this study to conduct experimental tests to develop non-dimensional relationships for prediction of scour hole and point bar dimensions.
General relationships: In river confluence, many variables can affect the scour hole and point bar dimensions. To developed general relation for predicting these dimensions, one may consider the following equations:
| (3) |
Applying dimensional analysis theory, the following non-dimensional equations can be developed:
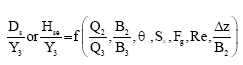 | (4) |
In these equations Q2 and Q3 are flow discharge in lateral channel and main channel downstream, respectively. B2 and B3 are the channel width of lateral channel and main channel downstream of confluence, respectively. θ is the confluence angle, So is the bed slope, Fg is the densimetric Froude number equal to V3/[g (Gs-1) D50]0.5 in which V3 is the flow velocity downstream of river confluence, g is the acceleration of gravity , Gs is the specific gravity of sediment, D50 is the median particle size and Re is the Reynolds number downstream of river confluence and is equal to ρV3Y3/μ in which ρ and μ are mass density and dynamic viscosity of water, V3 and Y3 are the flow velocity and flow depth downstream of confluence. Δz is the bed elevation difference.
Study of Gurram et al. (1997) showed that bed slope has no significant effect on flow pattern under subcritical condition. For high Reynolds number and rough boundaries, Reynolds number also have no effect on the flow pattern. In this study B2 and B3 were kept constant and Δz also were equal to zero. Therefore Eq. 4 is reduced to the following equation:
 | (5) |
Equation 5 is the basis equation for analysis of experimental data.
Experimental set-up: The experimental set-up consist of a main flume (9 m length , 35 cm width and 60 cm depth), a lateral flume (3 m length, 25 cm width and 60 cm depth). At the upstream end of each flume a stilling box has been installed to reduce the kinetic energy of the entrance flow. Discharge was measured by an electronic flow meter with an accuracy of 0.01 L sec–1. At the end of the main flume, a slide gate has been installed for controlling the downstream water depth. The lateral flume was connected to the main flume in three different confluence angles equal to 60, 75 and 90 degree. Figure 2 shows a plan view of the experimental set-up.
Experimental procedure: Once the lateral flume was connected to the main flume, the sediment bed material was placed on the bed of both flumes. Then the pump was started and flow allowed entering the main flume very slowly. During the filling of the flumes the tail water was closed. When the flow depth was high enough, the flow discharge was increased and at the same time the tail water was opened. When the discharge, in both flumes, is reached to the desired flow discharge, the tailwater was opened slowly till the flow depth was equal to the desired flow depth. This situation was kept constant for almost 5 h until the scour hole dimensions seems to be constant and the equilibrium condition is reached.
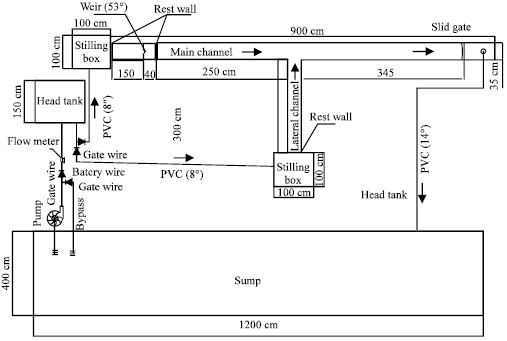 | |
| Fig. 2: | Plan view of the experimental set-up |
| Table 1: | Range of variables in this study |
 | |
| Table 2: | Summary of the experimental data obtained in this study |
 | |
| Table 3: | Values of non-dimensional parameters |
 | |
At the end the pump was shut down, the water was drained and the bed topography was measured.
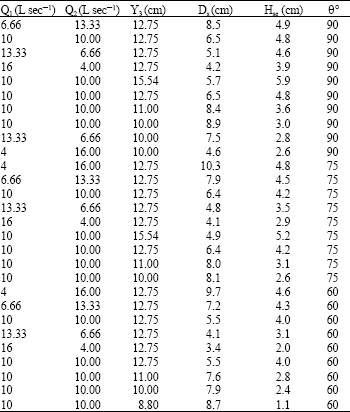
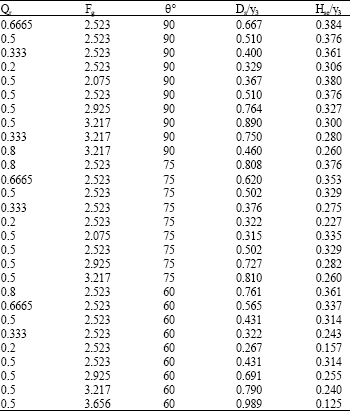
Experimental results: A significant quantity of local scour data and point bar dimensions were gathered during this study. Table 1 shows the range of variables conducted in this study. All of the experiments in which were conducted for the purpose of this study were relatively long in duration, thus the scour depths were at or very near the equilibrium condition at the end of each test. Table 2 shows summary of data obtained in this study. The values of non-dimensional parameters are also have been presented in Table 3.
As it was found, the ratio of Q2/Q3 or Qr has a significant affects on scour and sedimentation pattern. In this study five different discharge ratio (Qr) were studied. Figure 3 shows variation of relative scour depth (Ds/Y3) versus discharge ratio Qr for three confluence angles. As it can be seen from these figures, as Qr increases, the ration of Ds/Y3 increases. This is because as Q2 increases the separation zone dimensions increases pushing the main flow to the right bank, therefore the flow area in the main channel decreases and both flow velocity and bed shear stress increases. Figure 4 also shows variation of relative point bar height or Hse/Y3 versus discharge ratio Qr. The same trend can be seen in these figures. This is because as scour hole become larger, more sediment material washed out and therefore sediment material will be deposited further downstream creating point bar.
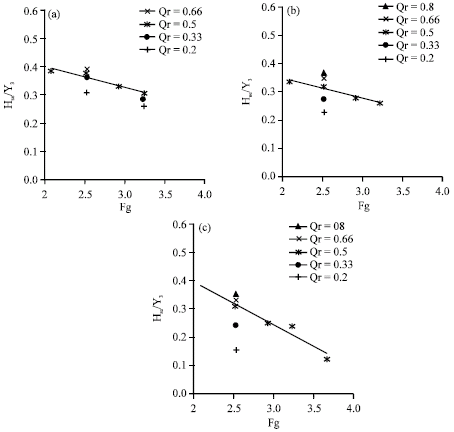
Effect of downstream densimetric Froude number on the scour and sedimentation pattern are shown in Fig. 5 and 6. Although the scour hole depth increases as Fg increases the point bar height is decreases as Fg increases. This is because as Fg increases, the flow potential for transporting sediment increases.
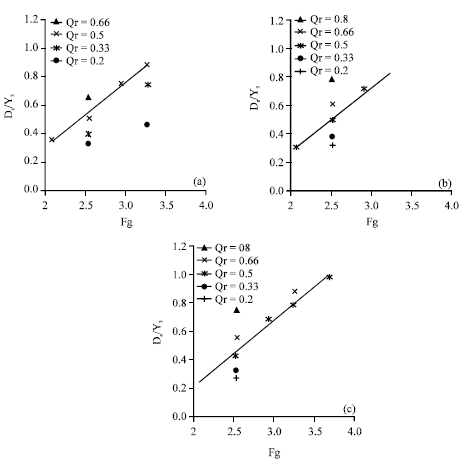
Variation of scour hole against confluence angle is shown in Fig. 7. As it can be seen from this figure, when θ increases the scour depth increases. This is because in small confluence angle the separation zone dimensions are small. For larger value of θ, the separation width increases causing more scour hole depth. The same trend can be observed from Fig. 8.
Developing scour prediction equation: One of the main objectives of the study was to provide an equation for predicting the scour hole depth. To do so, the equation that produced the best least-square fit to the data was found by analyzing experimental test as follow:
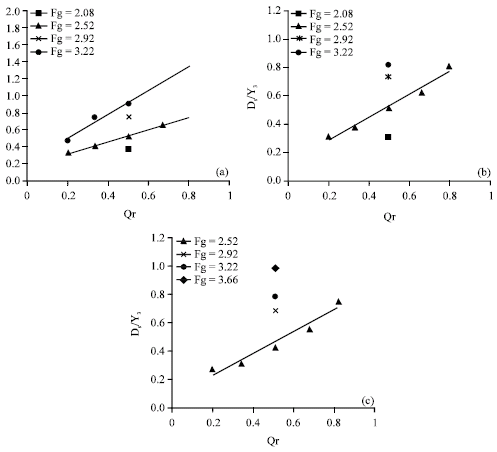 | |
| Fig. 3: | Variation of relative scour depth (Ds/Y3) versus discharge ratio Qr. a) θ = 90°, b)θ = 75° and c) θ = 60° |
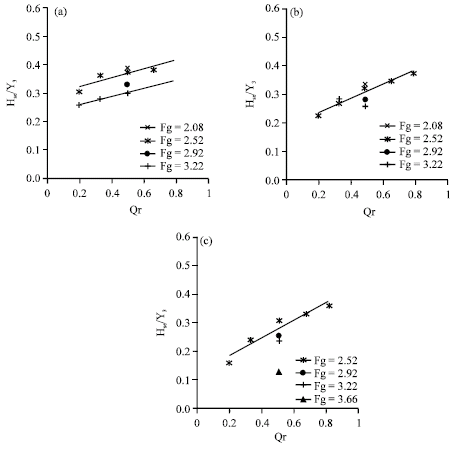 | |
| Fig. 4: | Variation of relative point bar height (Hse/Y3) versus discharge ratio Qr. a θ = 90°, b)θ = 75° and c) θ = 60° |
 | |
| Fig. 5: | Variation of relative scour depth (Ds/Y3) versus densimetric Froude number Fg, a) θ = 90° b)θ = 75° c) θ = 60° |
 | |
| Fig. 6: | Variation of relative point bar height (Hse/Y3) versus densimetric Froude number Fg, a), θ = 90°, b)θ = 75° and c) θ = 60° |
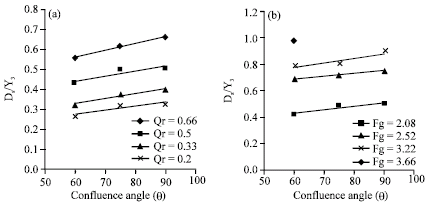 | |
| Fig. 7: | Variation of relative scour depth (Ds/Y3) against confluence angle (θ). a) for different Qr and b) for different Fg |
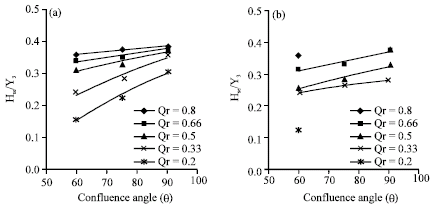 | |
| Fig. 8: | Variation of relative point bar height (Hse/Y3) against confluence angle (θ). a) for different Qr and b) for different Fg |
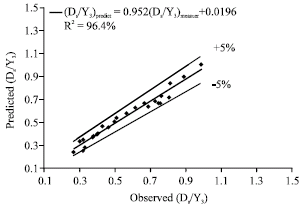 | |
| Fig. 9: | Observed values of relative scouring depth versus predicted values by Eq. 6 |
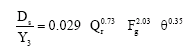 | (6) |
r = 98.2%
To investigate the accuracy of Eq. 6, observed values of relative scouring depth have drawn versus the predicted values and the results are presented in Fig. 9. As it can be seen from this figure, all of data are between the 95% confidence bands which means that Eq. 6 can be applied for prediction of relative scouring depth in river confluence. The sensitivity analysis of Eq. 6 shows that by variation of discharge ratio from 0.2 to 0.8, densimetric Froude number from 2.08 to 3.66 and confluence angle from 60 to 90 degree the mean values of relative scouring depth change 197, 87 and 13.5%, respectively. This means that in the process of scour in river confluence, the discharge ratio is the most important parameter not confluence angle which have been pointed out by other investigator such as Ashmor and Parker (1983) and Best (1988). The reason for their conclusion is that they have considered only the effect of confluence angle in their experimental results. It should be mentioned that comparison of Eq. 6 with Eq. 1 and 2 is not possible because of difference in experimental set-up and variables which have been considered.
Point bar height equation: To develop a relation for prediction of the height of point bar downstream of river confluence, following equation was obtained by analyzing the experimental data:
| (7) |
r = 92.3%
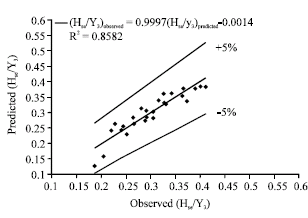 | |
| Fig. 10: | Observed values of depositional bar height versus predicted values by Eq. 7 |
To investigating the accuracy of Eq. 7, observed values of relative height of point bar have plotted versus the predicted values. Figure 10 shows the results. As it can be seen most of data are between the 95% confidence bounds which means the accuracy of Eq. 7 for prediction of relative height of depositional bar in river confluence is acceptable. On the other hand the sensitivity analysis of Eq. 7 shows that by variation of discharge ratio from 0.2 to 0.8, densimetric Froude number from 2.08 to 3.66 and confluence angle from 60 to 90 degree the mean values of relative height of depositional bar change 106, 77 and 42.6%, respectively. These results also show that relative discharge is an important parameter in the study of river confluence. Since previous works have not studied the point bar dimensions in river confluence, comparison with other investigators results is not possible.
The experiments conducted in this study have extended the scour and sedimentation data at river confluence. The most important non-dimensional parameters, especially the discharge ratio and the densimetric Froude number, on scour and sedimentation pattern were introduced. From the analysis of data it was found that:
| • | The ratio of lateral flow discharge to the downstream main channel discharge is the most important parameter in river confluence studies which must be considered. |
| • | As the discharge ratio, densimetric Froude number and the confluence angle increases, the scour depth increases. |
| • | A non-dimensional equation was developed which can predict the scour depth within 95% confidence. |
| • | The formation of point bar in river confluence was investigated and a non-dimensional equation was developed which can predict its height within 95% confidence. |
| • | Further field survey data can be conducted to test the application of these equations. |
This study is part of a research project which has been financially supported by Office of Irrigation and Drainage Research, Khuzestan Water and Power Authority, Iran. The authors would like to appreciate the reviewers of this paper for their valuable comments and suggestions.
NOTATION
| B2 | = | Lateral channel width. |
| B3 | = | Channel width downstream of confluence. |
| Ds | = | Scour depth. |
| D50 | = | Mean particle size. |
| Fg | = | Densimetric Froude number. |
| g | = | Acceleration of gravity. |
| Gs | = | Specific gravity of sediment. |
| Hse | = | Height of point bar. |
| Q2 | = | Lateral channel discharge. |
| Q3 | = | Discharge of channel downstream of confluence. |
| Qr | = | Discharge ratio (Q3/ Q2) |
| RDs | = | Relative scour depth. |
| Re | = | Reynolds number. |
| S0 | = | Bed slope. |
| V3 | = | Flow velocity downstream of confluence. |
| Y3 | = | Flow depth downstream of confluence. |
| θ | = | Angle of confluence. |