Research Article
LQ-Moment: Application to the Generlized Extreme Value
Department of Mathematic, Universiti Teknologi Malaysia, Johor, Malaysia
Abdul Aziz Jemain
Sciences Mathematic Studies Centre, Universiti Kebangsaan Malaysia, Malaysia
Mudholkar and Hutson (1998) introduced LQ-moments as a robust version of L-moments. The LQ-moments are constructed by using a class of robust location measures defined in terms of simple linear combinations of symmetric quantiles of the distribution of the order statistics, such as the median, trimean or Gastwirth, in places of expectations in L-moments. The LQ-moments are defined as
| (1) |
where
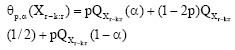 | (2) |
The linear combination, θp, a (.) is a quick measure of the location of the sampling distribution of the order Xr-k:r andQX (.) denotes the quantile estimator.
Mudholkar and Hutson (1998) found the performances of LQ-moments method depends on the quantile estimators and they suggested the kernel estimator or some quasi-quantile may be used in the estimation. They proposed the simplest quantile function estimator based on the Linear Interpolation Quantile (LIQ) to estimate the sample LQ-moments.
Ani and Aziz (2006) proposed the LQMOM based on the Weighted Kernel Quantile (WKQ) estimator to estimate the EV1 distribution parameters. The performances of the WKQ estimator of the EV1 distribution were compared with the estimators based on conventional LMOM, MOM (method of moments), ML (method of maximum likelihood) and LIQ estimator for various sample sizes and return periods. The results show that the LQMOM based on the WKQ performs better than LIQ, MOM and LMOM.
In this study, we focused on the chose the best quantile estimator of LQ-moments method to estimate the parameters of the distribution function. A popular quantile estimator namely the Weighted Kernel Quantile (WKQ) estimator, Harrell and Davis Quantiles (HDQ) estimators and the weighted HD quantiles (WHDQ) estimators will be used and compared with the LIQ estimator. We develop the method of LQ-moments for the Generalized Extreme Value (GEV) distribution, which is often employed in statistical analyses of hydrological data. Although the results for the GEV distribution cannot be directly transferred to other distributions, the conclusions drawn from this study should have general implications for the use of LQ-moments in hydrology. In order to determine which quantile estimator is the most suitable for the LQ-moment, Monte Carlo simulation is considered.
DEFINITION AND PROPERTIES OF LQ-MOMENTS
Let X1, X2,..., Xn be a random sample from a continuous distribution function F(.) with quantile function Q(u) = F-1(u) and let X1:n≤X2:n≤...≤Xn:n denote the corresponding order statistics. Hosking (1990) defined the rth L-moment λr as
| (3) |
Mudholkar and Hutson (1998) suggested a robust modification in which the mean of the distribution of Xr-k:r in (1) is replaced by its median or some others population location measure. In particular, they defined the rth LQ-moment ξr as
| (4) |
where 0≤α≤1/2,0≤p≤1/2. Examples of θp,a (.) are the median (p = 0, α = 1), the trimean (p = 1/4, α = 1/4) and Gastwirth (p = 0.3, α = 1/3). The three LQ-moments of the random variable X are defined as
| (5) |
| (6) |
| (7) |
The skewness based upon the ratios of LQ-moments to be called LQ-skewness is given by
| (8) |
Estimation of LQ-moments: For samples of size n, the rth sample LQ-moment ξr is given by
| (9) |
where the quick estimator θp,α (Xr-k:r) of the location of the order statistic Xr-k:r in a random sample of size r. The three sample LQ-moments from Eq. 9 are given by
| (10) |
| (11) |
| (12) |
where
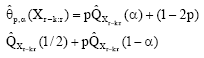 | (13) |
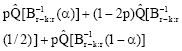 |
B-1 r-k:r (α) is the quantile of a beta random variable with parameter r-k and k+1 and ![]() denotes the sample quantile estimator.
denotes the sample quantile estimator.
THE QUANTILE FUNCTION ESTIMATOR
The sample quantiles estimators of the values of the population quantile Q(.), are used widely in a variety of applications such as a Q-Q plots and a box plot in the exploratory data analysis, non-parametric methods involving statistics such as the quartiles and their ranges, to theoretical topics such as density function estimation.
Let X1:n,≤X2:n≤...≤Xn:n be the corresponding order statistics. The quantile of a distribution is defined as
| (14) |
where F(x) is the distribution function (Hyndman and Fan, 1996).
A traditional estimator of Q(u) is the uth sample (David and Nagaraja, 2003) quantile given by
| (15) |
where [nu] denotes the integral part of nu. The sample quantiles experience a substantial lack of efficiency, caused by the variability of individual order statistics (Huang, 2001). Many authors use L quantile estimators to reduce this variability. A popular class of L quantile estimators is kernel quantile estimators has been widely applied (Sheather and Marron, 1990). But selection of kernel or bandwidth of the kernel estimators has always been a sensitive problem. Huang (2001) proposed an L quantile estimator namely quantile estimator HD performs as well as other L quantile estimators in large sample.
The estimation of population quantiles has been considered from a variety of viewpoints may be used (Sheather and Marron, 1990; Huang and Brill, 1999; Huang, 2001). Four quantile estimators are considered in the illustration of the proposed approach.
The linear interpolation quantile estimator: Mudholkar and Hutson (1998) proposed the simplest quantile function estimator based on the linear interpolation (LIQ). This quantiles is used commonly in statistical packages such as MINITAB, SAS, IMSL and S-PLUS. The LIQ estimator is given by
| (16) |
where ε = n’u - [n’u] and n’ = n+1.
The weighted kernel quantile estimator: A popular class of L quantile estimators is called kernel quantile estimators has been widely applied (Sheather and Marron, 1990). The L quantile estimators is given by
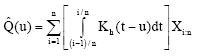 | (17) |
where K is a density function symmetric about 0 and
In this study, the approximation of the L quantile estimator is called as the weighted kernel quantile estimator (WKQ) proposed by Huang and Brill (1999) is considered. The WKQ is given by
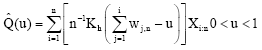 | (18) |
and the data point weights are
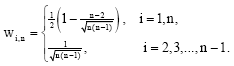 | (19) |
where K(t) = (2π)-1/2 exp(-1/2t2) is the Gaussian Kernel, h = [uv/n]1/2 is an optimal bandwith proposed by Sheather and Marron (1990) and v =1-u.
The HD-quantile estimator: Huang (2001) used the L quantile estimator to be called HD quantile estimators (HDQ), which not only gives better efficiencies but also avoids the problems of selection of kernel or bandwidth. The HDQ is given by
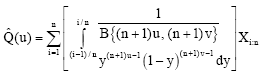 | (20) |
with v = 1-u, B(s, t) is the beta function with parameters s and t.
The weighted HD quantile estimators: Huang (2001) proposed a new estimator of the HD quantile estimator to be called the weighted HD quantile estimator (WHDQ). This quantile is more efficient in many cases, especially for the tails of the distributions and small sample sizes. The WHDQ is given by
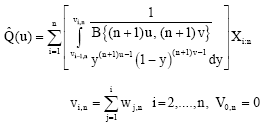 | (21) |
where and wi,n is given in (19).
GENERALIZED EXTREME VALUE
The Generalized Extreme Value (GEV) distribution, introduced by Jenkinson in 1955, has found many applications in hydrology. It was recommended for at-site flood frequency analysis in the United Kingdom, for rainfall frequency in the United States and for sea waves. For regional frequency analysis the GEV distribution has received special attention since the introduction of the index-flood procedure based on probability weighted moments (Martins and Stedinger, 2000). Many studies in regional frequency have used the GEV distribution (Hosking et al., 1985; Chowdhury et al., 1991). In practice, it has been used to model a wide variety of natural extremes, including floods, rainfall, wind speeds, wave height and other maxima. Mathematically, the GEV distribution is very attractive because its inverse has a closed form and parameters are easily estimated by L-moments (Hosking, 1990) and LQ-moments (Mudholkar and Hutson, 1998).
The GEV distribution has Cumulative Distribution Function (CDF)
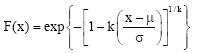 | (22) |
where ξ + α/k ≤x < ∞ for k < 0 and -∞ < x ≤ξ + α/k for k>0. Here μ, σand k are location, scale and shape parameters, respectively. Quantiles function of GEV distribution is given by
where
| (23) |
The LQ-moments of GEV distribution: The LQ-moment estimators for the GEV distribution behave similarly to the L-moments. From Eq. 4-7 and 2, the first three LQ-moment of the GEV distribution can be written as
| (24a) |
| (24b) |
| (24c) |
where
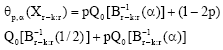 | (25) |
The LQ-moments estimators μ, σ and k of the parameters are the solution of 24a-c, when ξr are replaced by their estimators ξr. To obtain k we must solve by numerically solving the Eq. 8 given by
| (26) |
For ease of computation the following approximation equation with good accuracy has been constructed based on 24b, c and 8 as
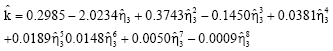 | (27) |
The ![]() unction is a very good approximation for
unction is a very good approximation for ![]() in the range (-1.0, 1.0). Once the value of k is obtained
in the range (-1.0, 1.0). Once the value of k is obtained ![]() and
and ![]() can be estimated successively from Eq. 24b and 24a as
can be estimated successively from Eq. 24b and 24a as
| (28) |
| (29) |
SIMULATION STUDY
A number of simulation experiments were conducted to investigate the properties of quantile estimators of LQ-moment for GEV distribution. Monte Carlo (MC) simulations were performed for sample sizes 15, 25, 50 and 100 and parameters of GEV are μ = 0 and σ = 1 with different values of k between -0.4 and 0.4. The samples are fitted by the GEV distribution function using the method of LQ-moment methods based on LIQ, WKQ, HDWQ and HDQ. The quick estimator, namely the trimean (p = 1/4, α = 1/4) is employed to estimates ![]() given by Eq. 12. For each sample size, 10,000 replicates were generated and quantile estimators of Q(F), F = 0.01, 0.1, 0.2, 0.5, 0.8, 0.9, 0.98, 0.99, 0.998 and 0.999, are examined in terms of the BIAS and RMS (root-mean-square error). The RMSE is an accepted criterion to compare alternative estimators of flood quantiles and shows in general the precision of particular estimator. The estimator with the lower RMSE is considered more precise. The sample RMSE is estimated by
given by Eq. 12. For each sample size, 10,000 replicates were generated and quantile estimators of Q(F), F = 0.01, 0.1, 0.2, 0.5, 0.8, 0.9, 0.98, 0.99, 0.998 and 0.999, are examined in terms of the BIAS and RMS (root-mean-square error). The RMSE is an accepted criterion to compare alternative estimators of flood quantiles and shows in general the precision of particular estimator. The estimator with the lower RMSE is considered more precise. The sample RMSE is estimated by
| (30) |
where N is the number of replicates of MC samples (10 000). Bias is defined as the difference between the expected value of the estimators and the true value. The estimator that exhibits the smallest bias (close to zero) is considered best. The sample bias is estimated by
| (31) |
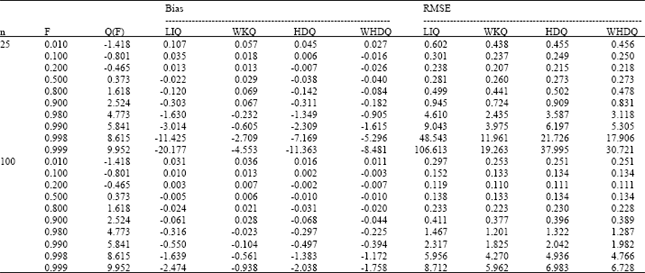
Table 1 shows the bias and RMSE of the F = 0.01-0.999 quantile estimators for LQ-moment methods based on LIQ, WKQ, HDWQ and HDQ estimators when k = -0.1.
| Table 1: | The bias and RMSE of the F = 0.01-0.999 quantile estimators for LQ-moment methods based on LIQ, WKQ, HDWQ and HDQ estimators for k = -0.1 |
 | |
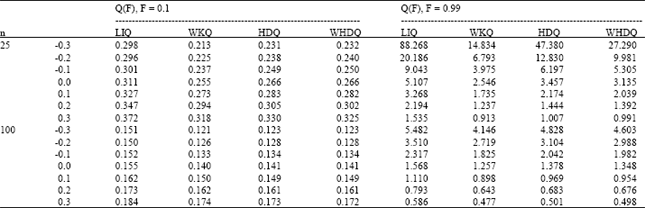
| Table 2: | RMSE of the 0.1 and 0.99 Quantiles, n = 25 and 100 |
 | |
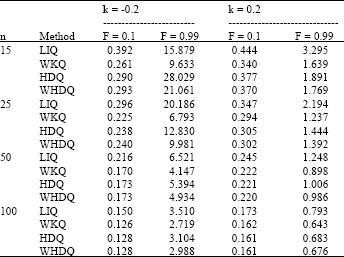
| Table 3: | RMSE of Quantile Estimators of GEV Quantiles |
 | |
In generally, the WKQ method always performs the best and the smallest bias and RMSE for any value of p. HDWQ estimator has the second smallest bias and RMSE followed by HDQ and LIQ estimators.
For different values of k the RMSE of LQ-moments based on the quantile estimators for the GEV distribution are determined and shown in Table 2 for samples sizes of 25 and 100.
For any values of k and sample sizes, the WKQ estimation has the smallest RMSE followed by the HDWQ, HDQ and LIQ estimators. For the Q(F), F = 0.99 quantile, the RMSE decreases as the sample size increases while for the Q(F), F = 0.10 quantile, the RMSE increases as the sample size increases for all methods while, but the performance of the WKQ is still the best. The LIQ estimator generally has a relatively higher RMSE for all samples.
Table 3 reports for k = -0.20 and 0.20, the RMSE of F = 0.1 and 0.99 quantile estimators for sample sizes of 15, 25, 50 and 100.
The Table 3 shows that WKQ was found to give results superior to the other estimators in all samples except for n = 50 and 100 for F = 0.1.
The GEV distribution has found wide application for describing annul floods, rainfall, wind speeds, wave heights, snow depth and other maximum is used in this study.
In this study, we compare the performance of WKQ, HDQ and WHDQ with the LIQ estimator proposed by Mudolkar and Hutson (1998) to estimate the sample of LQ-moments method to estimate the parameters of the GEV distribution. The Monte Carlo simulation was used in order to assess the accuracy of the quantile estimators.
Analysis results show that the WKQ has consistently performed better than the other quantile estimators. Although the linear interpolation quantile estimator available and commonly used in most statistical software packages, but it does not perform as well as WKQ to estimate the sample of LQ-moments for GEV distribution.