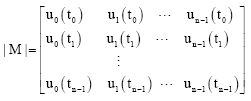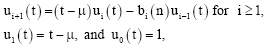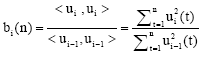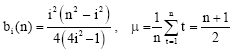Research Article
Face Recognition System Based on Orthogonal Polynomials
Department of Computer Science and Engineermg, Annamalai University Chidambaram, India-608002
R. Bhavani
Department of Computer Science and Engineermg, Annamalai University Chidambaram, India-608002