Research Article
The Lyapunov Exponents of the Impact Oscillator
Department of Electrical Engineermg, Far East College, 49 Chung-Hua Road, Hsin-Shih Town, Taman 74404, Taiwan
Impact dynamics is considered to be one of the most important problems which arise in vibrating systems. Such impacting oscillators may occur in the motion with amplitude constraining stops (Fig. 1). This problem has been researched in detail using bifurcation theory[1-7]. Different types of impacting response due to different ranges of driving frequency or control parameters can be predicted from bifurcation diagrams. In this study, calculation of the Lyapunov exponents for impact oscillator is considered. Lyapunov exponents measure the average divergence or convergence rate of nearby trajectories on a particular return map in space. If the largest Lyapunov exponent is positive the trajectory is chaos, whereas non-positive exponents indicate the trajectory is a stable motion. Thus the spectrum of Lyapunov exponents is one of the most useful diagnostics for systems.
Lyapunov exponents described the system’s behavior and provide the stability or instability of an equilibrium point of the non-linear system of the differential equation. For m-dimension system, with the mapping P: Rm, → Rm,
| (1) |
a small perturbation of this mapping tn → tn+δ tn, the Taylor expansion of Eq. 1 and the linearization model is
| (2) |
The stability at point tn is decided by the eigenvalues of the Jacobian matrix DP(n)(tn). The Lyapunov exponents measure the average rate of the convergence or divergence of the system and are defined by many researchers[8-10].
| (3) |
Thus m exponents of the average rate λm can be calculated if the Jacobian matrix is available.
In general, if the underlying dynamic system is smooth, then the spectrum of Lyapunov exponents can be calculated using the Poincare return map[10]. For example, a three dimensions flow in (t, x, v) space, the solutions can be projected onto a particular section t = ψ, where ψ is a constant in [0, T = 2π/ω]. Thus a two-dimensional Poincare map is defined by a difference equation,
| (4) |
where, x, v are vectors and f, g are non-linear transformations. The Jacobian matrix is expressed as:
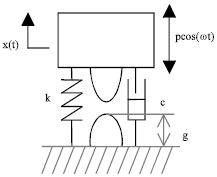 | |
| Fig. 1: | Impact oscillator |
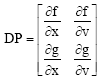 | (5) |
In the current problem of the impact oscillator under consideration is non-smooth due to the amplitude constraint. Thus the equation of the Poincare map is non-smooth when impact occurs and the derivative in Eq. 5 is not defined[11-14]. To overcome this problem the impact map is considered to develop the algorithms.
MATHEMATICAL MODEL
The impact oscillator is considered in Fig. 1, where the system is under a harmonic excitation with an amplitude constraint. The impact oscillator is governed by the following equation
| (6) |
where, ![]() , x are the acceleration, the velocity, the displacement and m, c, k, p, ω, g are the mass, the damping, the stiffness, the forcing amplitude, the forcing frequency, the amplitude constraint, respectively. The impact occurs whenever x = g and the velocity is modeled by
, x are the acceleration, the velocity, the displacement and m, c, k, p, ω, g are the mass, the damping, the stiffness, the forcing amplitude, the forcing frequency, the amplitude constraint, respectively. The impact occurs whenever x = g and the velocity is modeled by ![]() , where the t+ represents the time after impact, the t¯ represents the time before impact and r is restitution coefficient. For simplicity, we set m = 1, c = 0, k = 1 and p = 1 then the system convert to
, where the t+ represents the time after impact, the t¯ represents the time before impact and r is restitution coefficient. For simplicity, we set m = 1, c = 0, k = 1 and p = 1 then the system convert to
| (7) |
With initial conditions x(t0) = x0 and ![]() , the solution of the displacement x and the velocity v between impacts are:
, the solution of the displacement x and the velocity v between impacts are:
| (8) |
| (9) |
where, z = 1/(1-ω2).
JACOBIAN MATRIX FOR IMPACT MAP
To obtain the difference equation of Eq. 1, the variables xn, vn and tn are considered as the impact n, then the variables xn+1, vn+1 and tn+1 are obtained from Eq. 8 and 9 for the initial conditions
| (10) |
Thus the difference equations can introduce as below:
| (11) |
| (12) |
where, xn+1 = xn = g. Thus the impact return map can be constructed from a three dimensions flow in (t, x, v) space onto a two dimension map (t,v) when x = g. Using Eq. 11 and 12, the Jacobian matrix for impact map can be derived[1,2],
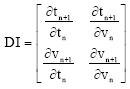 | (13) |
The components in Eq. 13 are:
 | (14) |
| (15) |
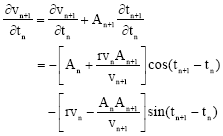 | (16) |
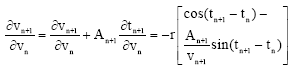 | (17) |
where,
| (18) |
are the accelerations at the two impacts.
LYAPUNOV EXPONENTS
Using the Jacobian matrix of Eq. 13 and the definition of Eq. 3, two Lyapunov exponents of impact oscillator can be obtained by:
| (19) |
In computation of the eigenvalues of the matrix J, that is given by:
| (20) |
Only a few iterations, the matrix J becomes very large for chaotic case and null for the periodic case because the product of the matrix DI in Eq. 20. To overcome this problem, the QR-factorisation technique applied[15-17]. Given a matrix A, there is a unique factorization
| (21) |
where, R is a square right upper triangular matrix and Q has orthogonal columns. Consider an arbitrary orthogonal matrix Q0 and apply the orthogonalisation procedure to the impact map
| (22) |
The columns Q1 are now an orthogonal basis for the impact map at n = 1 and R0 gives the relationship between this map and the image of the Q0 under the Jacobian matrix DI(1). This process can be repeated recursively and gives:
| (23) |
Thus the calculation of the Lyapunov exponents in Eq. 19 is converted to the summation of the matrix In(Rj) in Eq. 24.
| (24) |
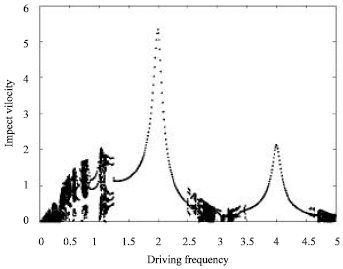 | |
| Fig. 2: | Bifurcation diagram of the impact oscillator under the parameters m=1, c=0, k=1, p=1, r=0.8 and g=0 |
 | |
| Fig. 3: | Estimated Lyapunov exponents of the impact oscillator under the parameters m=1, c=0, k=1, p=1, r=0.8 and g=0 |
The result shown in Fig. 2 is the plot of bifurcation diagram for varying the driving frequency; the regions of the stable and unstable oscillator are demonstrated by points set in impact map. The corresponding results of the estimated Lyapunov exponents are shown in Fig. 3, where the positive values indicate the stable motions and the non-positive values indicate unstable motions. For example, the results in Fig. 4a show periodic points set in impact map. The corresponding results of the estimated Lyapunov exponents are shown in Fig. 4b, where both exponents converge to non-positive values after 5000 iterations. This indicates that the impact oscillator is stable at driving frequency ω = 2.
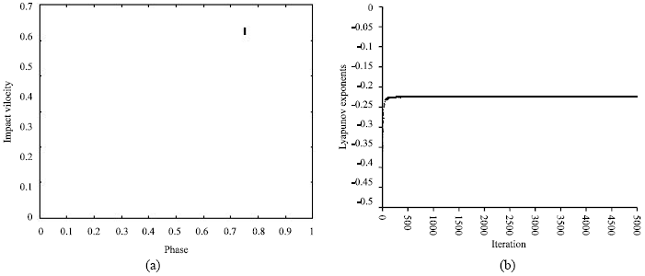 | |
| Fig. 4: | Impact oscillator under the parameters m=1, c=0, k=1, p=1, r=0.8, g=0 and ω=2 (a) impact map (b) Lyapunov exponents |
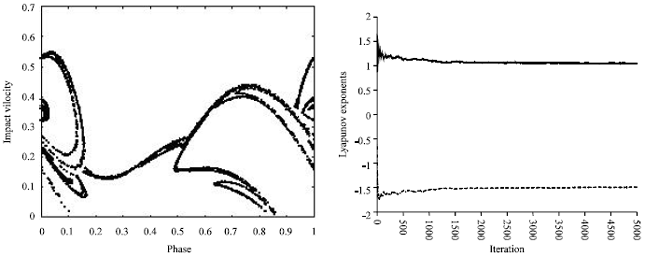 | |
| Fig. 5: | Impact oscillator under the parameters m=1, c=0, k=1, p=1, r=0.8, g=0 and ω=2.8 (a) impact map (b) Lyapunov exponents |
For the case of driving frequency at ω = 2.8, the results show strange points set in Fig. 5a and one of the estimated Lyapunov exponents converges to a positive value in Fig. 5b. This confirms that the impact oscillator is unstable.
The algorithm of computing Lyapunov exponents is successfully applied to the impact oscillator. The impact oscillator is considered as non-smooth dynamic system; therefore the Jacobian matrix for impact map is derived. The results show the plot of bifurcation diagram consists with the estimated Lyapunov exponents for varying the driving frequency.