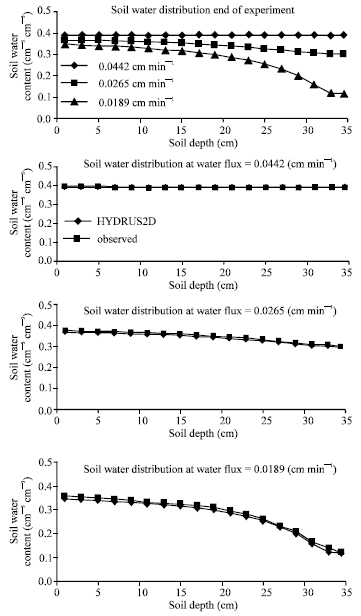
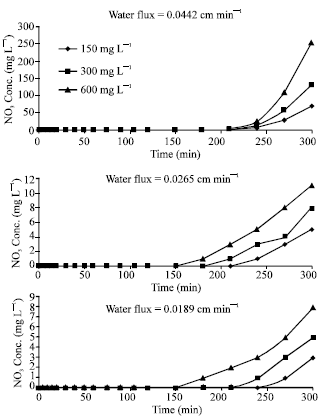
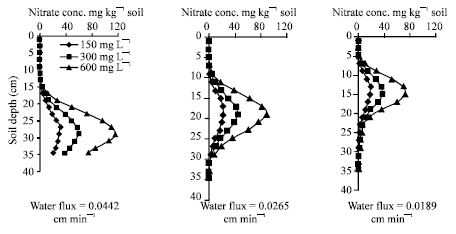
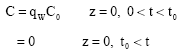Research Article
Nitrate Leaching Through Unsaturated Soil Columns: Comparison Between Numerical and Analytical Solutions
Department of Soil Science, College of Food and Agriculture Sciences, King Saud University , P.O. Box 2460, Riyadh 11451, Saudi Arabia
G. Abdel- Nasser
Department of Soil Science, College of Food and Agriculture Sciences, King Saud University , P.O. Box 2460, Riyadh 11451, Saudi Arabia