Research Article
Comparison of the One-Dimensional and Two-Dimensional Arterial Models
Department of Mathematics, University of Benin, Benin City Nigeria
Christopher E. Omole
Department of Mathematics, University of Benin, Benin City Nigeria
The advent of mathematical modeling was introduced through the work of Frank in 1899 who introduced the Windkessel model as a mathematical tool for describing the arterial pulse waves. Over the decades the bug has caught on and many useful deductions and insights have been made using this tool. There have been various models ranging from the one dimensional; linear and non-linear models (Anliker et al., 1974; Kivity and Collins, 1974a,b; Hoogstraten and Smit, 1978; Oghre and Akinrelere, 2000). There have been two-dimensional models (Wormerseley, 1955; Lou, 1975; Santabrata and Prashanta, 2000) and the three dimensional models (Rao and Devanathan, 1973; Krijger et al., 1981). Every one of these models had been very useful to the understanding of the arterial tree.
There is no exact model that can represent all arterial properties nor can we reproduce the complete arterial tree because experimental verification of complex model parameters will be tedious and conceptual understanding of the vessel response is still clouded. Also physiological data on arteries are still too limited to permit a model of great details.
However the basic properties of a useful mathematical model is that the model generates waveforms, which are free from artifacts resulting from the models itself or from the computational techniques. The assumptions on which the model is based should be realistic and related to the problem. Thus the choice of model, its degree of complexity and computational scheme of solution are crucial to the model.
In this study we compare the usual one-dimensional and two-dimensional models of the arterial tree to ascertain which of these better describes the characteristics of the arteries.
MATHEMATICAL FORMULATION
One-dimensional equation: The vessel is assumed to be circular, isolated and elastic. Blood is approximated as a Newtonian, fluid of constant viscosity and density, incompressible flow described by the Navier-Stoke equations. The pressure amplitude is assumed small and its wavelength long relative to the vessel radius. Blood flow is laminar and velocity profile can generally be considered radially axi-symmetric. Under the assumption of one dimensionality the control theory gives the continuity equation as
| (1) |
where A denotes the cross sectional area of the artery, u the axial blood velocity (average over the cross-section), x the axial coordinate and t is the time. The first term is the rate of storage of blood within the arterial segment; the second is the difference between the blood flowing into and out of the segment in the axial direction.
The second fluid dynamics relation is the momentum equation, which balances inertia, friction and pressure forces acting on the blood. In one dimension it is given as
| (2) |
where P is the pressure difference across the tube and ρ is the fluid density. The first term is the acceleration of the blood; the second is the convective acceleration due to axial rate of change of velocity, the third the pressure gradient and the fourth term represents the friction at walls of the arteries.
Although the shear stress in pulsating flows is not directly related to the instantaneous mean velocity, it is assumed to be given by the laminar Poiseuille relation
| (3) |
where μ is the blood viscosity.
Eq. 4 then becomes
| (4) |
It is assumed that the lumen area is related instantaneously to the pressure (Vander Werff, 1974) and there is no phase lag; thus the one dimension state equation is given as
| (5) |
We shall consider later Eq. 1, 4 and 5.
Two-dimensional equations: For the two dimensional equation we use the cylindrical coordinate system (r, θ, x) with the x axis aligned with the local vessel axial direction. The velocity in the circumferential direction is assumed to be zero. This removes any dependency on θ within the model. Thus the Navier-Stoke equations which govern Newtonian fluid flow reduce to (Lou, 1975; Smith et al., 2002)
| (6) |
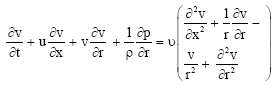 | (7) |
In Eq. 6 and 7 x and r are the axial and radial directions respectively while u and v are the axial and radial velocity. The pressure is denoted by p, kinematic viscosity by and density by. The first terms in each of Eq. 6 and 7 are the acceleration in the respective axial and radial direction, the next two terms are the convective acceleration while the last terms are the pressure term while the terms on the right sides the viscous terms are represented. The conservation of mass in two-dimensional is given by:
| (8) |
We adopt the dimensional analysis of Smith et al. (2002) as follows:
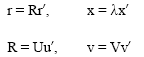 |
| (9) |
where U and V are characteristic axial and radial velocities and λ is a characteristic length defined by λ = RU/V where R is the characteristic inner vessel radius.
Using these transformation Eq. 6 and 7 become
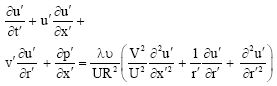 | (10) |
 | (11) |
If we assume that the radial velocity is small compared to the axial velocity then terms multiply by V2/U2 can be neglected and Eq. 10 becomes:
i.e.,
| (12) |
Eq. 11 also becomes:
| (13) |
Equation 13 implies that the pressure is constant across the vessel cross section. The continuity Eq. 8 can also be transformed and written in the form:
 | (14) |
The continuity Eq. 8 can also be transform and written in the form:
| (15) |
If we introduce a non-dimensional inner radius quantity and integrate Eq. 14 and 15 from r’ = 0 and r’ = R’ we have:
 | (16) |
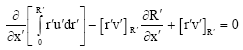 | (17) |
Since the wall is a streamline surface,
| (18) |
or
| (19) |
If we define the average axial velocity to be:
| (20) |
and the non-dimensionalized energy quantity α’ as:
| (21) |
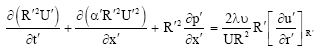 | (22) |
| (23) |
If we make a transformation back to the dimensional quantity as r = RR’ and ru = UU’ Eq. 22 and 23 can be written as:
| (24) |
| (25) |
If we assume a velocity profile of the form (Smith et al., 2002)
 | (26) |
If we substitute Eq. 26 into Eq. 21 we have
| (27) |
thus Eq. 24 becomes:
| (28) |
COMPARISM OF THE ONE DIMENSIONAL MODEL AND THE TWO DIMENSIONAL MODEL
We shall now consider Eq. 4 and 28. For each of these equation we require another equation which describes the mechanics of the vessel by relating pressure with the cross sectional area. We adopt an empirical relationship between transmural pressure and the radius (or cross-sectional area) of the form (Fung, 1997)
| (29) |
where R0 is the vessel radius at zero pressure and β is the compliant constant of the vessel. This Equation can be written in the form
| (30) |
This pressure-area relation is similar to that proposed by Olufsen (1999) with only one parameter β. Then
| (31) |
Let us also consider the steady state by setting all transient terms in Eq. 4 and 28 to zero then we have:
| (32) |
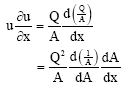 | (33) |
If we consider a given constant flow rate Q, the conservation of mass Eq. 1 and 25 imply that velocity u can be expressed as:
| (34) |
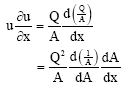 |
| (35) |
If we substitute Eq. 31 and 35 into Eq. 32 and 33 we have:
| (36) |
| (37) |
Equation 36 and 37 are virtually the same except for some constant and both can be integrated by separable variable method to determine the value of x as:
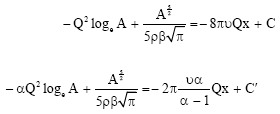 |
This shows that the one-dimensional model and the two dimensional model lead to the same determination of the site x when steady state of flow is consider. In each case the coefficient of x is the measure of the viscous term. Thus we conclude that the use of one-dimensional model which is easily solvable analytically is as dependable as the two dimensional model.