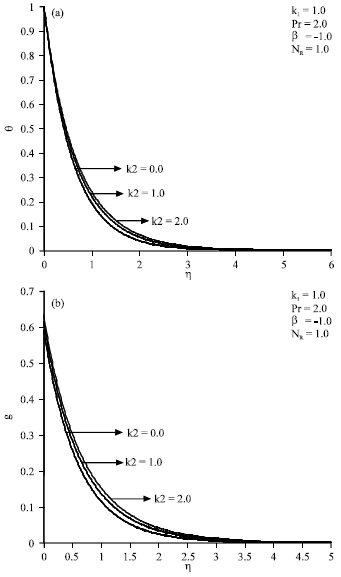
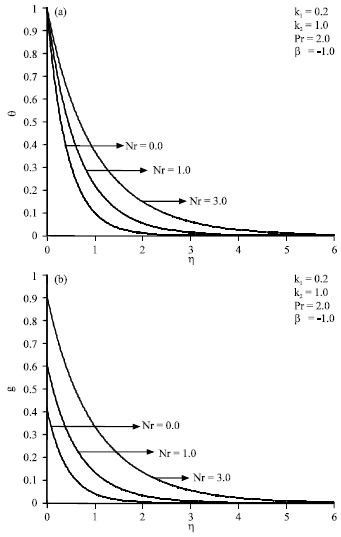
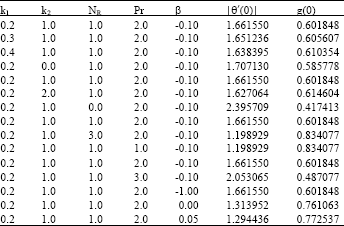
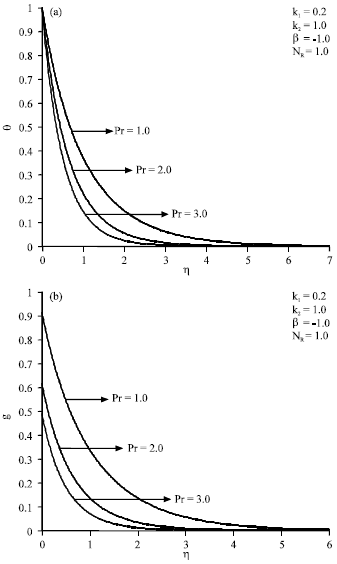
Research Article
Effect of Radiation on the Flow of a Visco-Elastic Fluid and Heat Transfer in a Porous Medium over a Stretching Sheet
Department of Mathematics, Anna University, Chennai, India
P. Anuradha
Department of Mathematics, Jerusalem College of Engineering and Research Scholar, Anna University, Chennai, India