ABSTRACT
This study presented Fuzzy Logic Methodology for Evaluating Alternatives (FLMEA) to compare between different power production systems. The FLMEA enabled us to condense large amount of data into a smaller set of fuzzy variable rules. Also FLMEA method used minimum and maximum operations which are easier and faster than average and sum operations that are used by other methods. The fuzzy method was applied to perform a comparison between different production options of power systems in Jordan. The results were compared to those obtained using neuro-fuzzy method, which is considered to be a slower learning technique than the fuzzy sets methodology.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2006.2117.2125
URL: https://scialert.net/abstract/?doi=jas.2006.2117.2125
INTRODUCTION
This study used fuzzy logic method to determine the most preferable option or options to produce electricity and give solutions to some of the problems Jordan is facing now and in the future. Other methods can be used, but fuzzy logic method is superior over other methods in terms of speed and ease of application. Applying fuzzy approaches to real problems is an effective alternative to traditional methods, like the analytic hierarchy process (Saaty, 1980, 1988). The results were compared to those obtained by neur-fuzzy methodology (Mamlook et al., 2001a), which is considered to be a little slower learning technique than the fuzzy sets methodology.
The energy development options in Jordan are under study by researchers and governments. Electrical power is produced in Jordan using fossil fuel, but this option is not preferable since Jordan's spending on petroleum is more than 50% of export earning. Also using fossil fuel does not give solutions to the problems facing Jordan from environmental problem to unemployment. Therefore, there is a need to look at other electricity options. More information on electricity power production options in Jordan are outlined in Appendix A.
The term fuzzy logic has been used in narrow and broad senses. The broad sense of fuzzy logic includes the narrow sense of fuzzy logic as a branch. In a narrow sense, fuzzy logic system is a logic system that generalizes classical two-valued logic for reasoning under uncertainty. In a broad sense, fuzzy logic refers to the technologies and theories that use classes with unsharp boundaries (fuzzy sets). Other areas include fuzzy arithmetic, fuzzy probability theory, fuzzy control, fuzzy decision analysis, fuzzy topology, fuzzy neural network theory, fuzzy mathematical programming and fuzzy pattern recognition, etc. In all these areas, a conventional black-and-white concept is generalized to a matter of degree. By doing this, one accomplishes two things: (1) improved ability to develop a cost-effective solution to real-world problems and (2) effortlessness of describing human knowledge involving vague concepts. Even though the broad sense of fuzzy logic covers a wide range of theories and techniques, its main technique is based on four basic concepts: (1) fuzzy if-then rules: a knowledge representation scheme for describing a functional mapping or a logic formula that generalized an implication in two-valued logic; (2) possibility distributions: constraints on the value of a linguistic variable imposed by assigning it a fuzzy set; (3) fuzzy sets: sets with smooth boundaries and (4) linguistic variables: variables whose values are both qualitatively and quantitatively described by a fuzzy set. The first concept is important because it is the basic for most industrial applications of fuzzy logic developed to date, including many fuzzy logic control systems. The other three concepts are fundamental for all subareas in fuzzy logic. More detail on fuzzy logic theory and applications are outlined in (Zadeh, 1965; Mamlook et al., 1999; 2001b, 2005; Malook and Al-Jayyousi, 2003).
After Zadeh's work on fuzzy sets (Zadeh, 1965), many theories in fuzzy logic were developed in Japan, Europe, United States and elsewhere. Since the 1970s Japanese researchers have been advancing the practical implementation of the fuzzy logic theory; they have been commercializing this technology and they have now over 2000 patents in the area from fuzzy air conditioner, fuzzy washing machine, fuzzy toasters, fuzzy rice cookers, fuzzy vacuum cleaner and many other industrial fuzzy control processes. They have a subway system that is totally controlled by fuzzy computer. It is smooth enough that riders do not need to hold straps and the controller makes 70% fewer judgmental errors in acceleration and braking than human operators. The US Space Administration has been involved in the use of fuzzy logic in space control decision making. Energy consumption could be analyzed using fuzzy sets (Oder et al., 1993). Also systems could be controlled using fuzzy rules (Mamlook et al., 1999).
FUZZY SET METHODOLOGY FOR EVALUATING ALTERNATIVES
In order to compare objects (options) which are fuzzy, vague, or ambiguous we introduce a special notion of relativity (Shimura, 1973). Let p and q be variables defined on universe U and define two pairwise functions, fq(p) and fp(q) as the membership functions of q with respect to p and p with respect to q, respectively. Then to do the measurement of the membership value of choosing p over q, we use the relativity function that is defined such as:
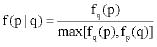 | (1) |
This relative function f(p|q) can be used as the membership of preferring p over q. For more than two variables, we define variables p1, p2, …, pi, pi+1, …, pm on the universe U, let these variables be collected on the set S; S ={ p1, p2, …, pi, pi+1, …, pm} and form a matrix of relativity values, f(pi |qj) where i, j = 1,2,…, m and pi and qj are defined on the universe U. This matrix will be an m by m matrix and called the C matrix (C for comparison). This matrix can be used to rank many different fuzzy sets.
In order to determine the overall ranking, we find the largest or smallest values in each of the rows of the C matrix; i.e.,
| (2) |
or
| (3) |
where Cj’ or Cj” is the membership ranking value for the jth variable. The present study use the maximum function when we are ranking different objects (options) in terms of their benefits and the minimum function is used when different objects (options) are ranked in terms of their costs.
A description (D) of fuzzy sets, as a methodology for evaluating alternatives (FLMEA) is outlined below (Mamlook et al., 2001a).
| • | The first step involves the composition or sustaining of the components of the problem or issue to be analyzed. This phase may involve a group decision making to explore the various perspectives of the problem. In this study, the fuzzy method was composed of the following levels: goals, systems and factors. However, these components are by no means exhaustive; other levels may be incorporated into the method such as strategies, scenarios and/or characteristics. |
| • | The second step is to make pairwise comparisons; i.e., to compare the elements of a problem in pairs (as will be shown in the numerical example below) against a given goal or criterion. To perform pairwise comparisons, a matrix is used to compare different variables; this is done as follows: |
| • | Start at the top of the problem=s structure to select the factor (F), that will be used for making the first comparison. Then, from the level immediately below, take the elements to be compared for example, P1, P2, P3, . . ., PM. Considering that we have M elements; arrange these elements in a matrix as shown in Table D1. |
| • | In this matrix compare the element P1 in the column on the left with P1, P2, P3 and so on in the row on the top with respect to factor F in the upper left-hand corner. To compare elements, one should ask: How much more strongly does this element possesses or contributes to influence, satisfy, or benefit the property than does the element with which it is being compared? |
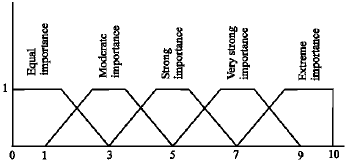 | |
| Fig. 1: | Fuzzy pairwise comparison values |
| Table D1: | Sample matrix for fuzzy pairwise comparison |
 | |
| Table D2: | Simple fuzzy matrix comparing three elements for factor F |
 | |
| Table D3: | Fuzzy relative weights for three elements |
 | |
| Table D4: | Simple fuzzy comparing 3 elements against each other |
 | |
| Table D5: | Fuzzy relative weights for three factors |
 | |
| • | To fill the matrix of pairwise comparisons, we may use the five fuzzy values shown in Fig. 1. When comparing one element in a matrix with itself, the comparison must give unity (1) which represents the values in the diagonal of the matrix. |
| • | To illustrate how to form a normalized matrix and to come up with relative weights in a generalized form, the following numerical example is presented: Suppose that the outcome of pairwise comparison was made for three elements P1, P2 and P3 with respect to factor F as shown in Table D2. |
To harmonize our judgments so as to get relative weights, the following steps are to be taken:
| • | Divide each entry in each column by the maximum value of that column to obtain the normalized matrix as shown in Table D3. |
| • | Determine minimum (maximum) value in each row depending on finding weights based on cost (benefit); this yields the percentages of overall relative priorities of the elements P1, P2 and P3. Hence, the study make deductions with reference to relative weights as calculated above. |
| • | Construct the weights of the factors against each other as shown in Table D4 and Table D5. |
APPLICATION OF THE FLMEA
The fuzzy logic decision selection of best electrical production option(s) in Jordan was applied according to their costs and benefits (Table B1 and B2 in Appendix B). Data in Table B1 and B2 are actual data obtained from (National Electric Power Company in Jordan, 2005). Separately, we considered the benefits (Fig. 2) and the costs (Fig. 3). Figure 2 and 3 are based on actual data obtained from (National Electric Power Company in Jordan, 2005). The cost-to-benefit ratios were also obtained. The objective of the present study is to make the decision selection of the best electrical production options that cost less and have the most benefits.
The fuzzy logic was used to compare benefits of the electrical production options (p1 = nuclear; p2 = wind; p3 = solar; p4 = hydro; p5 = fossil fuel) in Jordan to decide which option has the preferable benefits. Many factors affect this decision. They include efficiency, reliability, availability of fuel, national economy, social benefits and safety (Fig. 2). First, pairwise membership functions fpi(pj), i, j = 1, 2, 3, 4, 5, were determined using five fuzzy values (Zadeh, 1972), as shown in Fig. 1. These values represent the subjective benefits of appropriateness of each electrical production option when compared only one to another (Table 1). Equation 1 calculate all of the relative values, Table 2 expresses these calculations, this is the comparison (C) matrix. The additional column to the right of the C matrix is the maximum value of each rows (relative weights); Cj’, j = 1, 2, 3, 4, 5 in Eq. 2. Table 3 is determined using pairwise membership functions for all benefits criteria with respect to each other. Table 4 is determined using Eq. 1 and 2 to obtain the relative weights. The overall relative weight factor was then obtained from the results of Table 2 and 4. Table 5 shows how these relative weights factors were calculated.
The fuzzy logic was then used to compare costs of the electrical production options (p1 = nuclear; p2 = wind; p3 = solar; p4 = hydro; p5 = fossil fuel) in Jordan to decide which option has the lowest cost. Many factors affect this decision, including cost of fuel, hardware cost, maintenance and service, auxiliary system and environmental constraints (Fig. 3). First, pairwise membership functions fpi(pj), i, j = 1, 2, 3, 4, 5, were determined using five fuzzy values (Fig. 1). These values represent the subjective cost appropriateness of each electrical production option when compared one to another (Table 6). Equation 1 was then used to calculate all of the relative values. Table 7 expresses these calculations, this is the comparison (C) matrix.
| Table 1: | Fuzzy relational values of electrical production systems with respect to benefits |
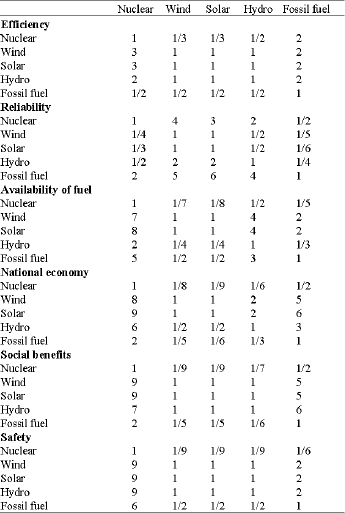 | |
| Table 2: | Fuzzy relative weights of electrical production systems with respect to benefits |
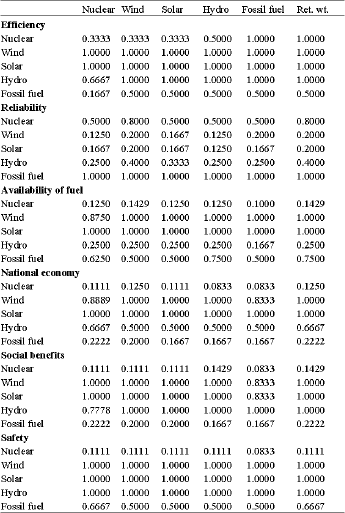 | |
| Table 3: | Fuzzy relational values for optimum benefits against each other |
 | |
| Table 4: | Fuzzy relative weights for optimum benefits against each other |
 | |
| Table 5: | Overall fuzzy relative weights for optimum benefits |
 | |
| * Normalized relative weight = Relative weight/maximum relative weight | |
| Table 6: | Fuzzy relational values of electrical production systems with respect to cost |
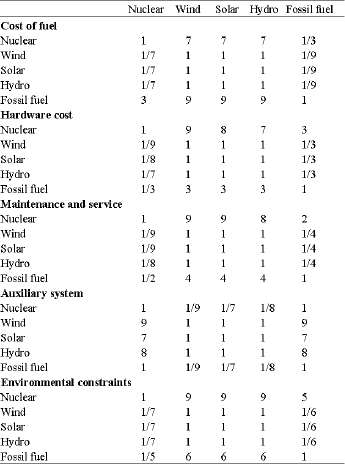 | |
| Table 7: | Fuzzy relative weights of electrical production systems with respect to cost |
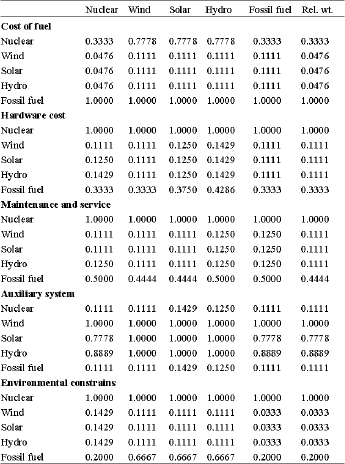 | |
| Table 8: | Fuzzy relational values of electrical production systems with respect to cost |
 | |
| Table 9: | Fuzzy relative weights for optimum costs against each other |
 | |
| Table 10: | Overall fuzzy relative weights for optimum costs |
 | |
| * Normalized relative weight = Relative weight/maximum relative weight | |
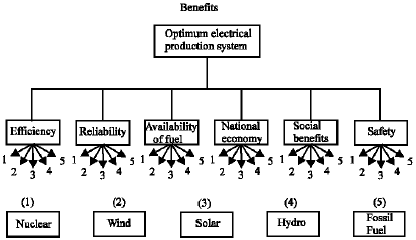 | |
| Fig. 2: | Benefits fuzzy structure |
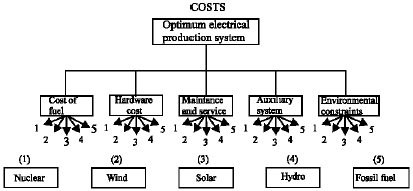 | |
| Fig. 3: | Costs fuzzy structure |
The extra column to the right of the C matrix is the minimum value of each row; Cj”, j = 1, 2, 3, 4, 5 in Eq. 3. Table 8 is determined using pairwise membership functions for all benefits criteria with respect to each other. Table 9 is determined using Eq. 1 and 3 to obtain the relative weights. The overall relative weight factor was then obtained from the results of Table 7 and 9. Table 10 shows how these relative weight factors were calculated.
RESULTS AND DISCUSSION
The fuzzy sets enabled us to condense large amount of data, collected to compare between the five electrical production systems in Jordan, into a smaller set of variable rules (Appendix B, Table 1 and 6 Fig. 1). From the results (Table 5 and 10), one can note that the preferable option is to use solar system to produce electricity in Jordan. The next two options are the use of wind system and hydro system. Solar, wind, hydro, or all these three options could be used to produce electricity in Jordan with minimum cost, as presented by Table 7 and optimum benefits in terms of issues related to availability of fuel, national economy, social benefits and safety (Table 2).
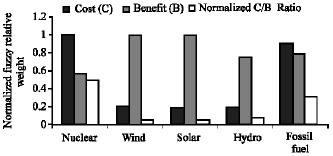 | |
| Fig. 4: | Electricity production system |
To obtain normalized cost-to-benefit ratios, the overall fuzzy cost relative weights (Table 10) were divided by the overall fuzzy benefits relative weights (Table 5), these ratios were then normalized to have better comparison between the five electrical production options in Jordan, as shown in Fig. 4. From Fig. 4, one can note that solar option comes first, followed by wind, hydro, fossil fuel and then the least option is nuclear system due to its high initial cost and safety factor.
CONCLUSIONS
One of the advantages of the Fuzzy Logic Methodology for Evaluating Alternatives (FLMEA) presented here is that it uses fuzzy sets that enabled us to condense large amount of data into smaller set of variable rules. Also FLMEA method used minimum and maximum operations which are easier and faster than average and sum operations that are used by other methods, for example the method used in (Akash et al., 1999). Based on FLMEA method, the solar electrical production option was the best preferable option that can be used to produce electricity in Jordan. The second and third options were wind and hydro systems. In conclusion, Jordan has option of using solar, wind, hydro, or the use of these two or three options combined to produce electricity. These results agreed with those obtained in a recent study by the authors using a different methodology known as the analytical hierarchy process (AHP) (Akash et al., 1999). Similarly, the fuzzy sets methodology outlined in this study was also used in another paper on the evaluation of solar systems (Mamlook et al., 2001b). The results of this study show that this method can be used in number of applications and it is not sensitive to the real input data. On the other hand they are sensitive to the relationship of one cost (or benefit) relative to the other. When comparing the results of this methodology to those obtained using neuro-fuzzy method (Mamlook et al., 2001a), which is considered to be a slower learning technique than the fuzzy sets methodology, the study found them to be consistent (Table 5 and 10) (Mamlook et al., 2001a).
APPENDIX A
Electricity power production options in Jordan: Solar energy can be used in the production of electricity (Haj-Khalil et al., 1997; Kolb, 1998; Kribus et al., 1998; Trieb and Nitsch, 1998). This technology can be applied to Jordan, since Jordan has over 300 sunshine days per year. Technology suggests that the Dead Sea can be used as a 450 km2 solar lake, producing a 2500 MW (Murakami and Wolf, 1995). are number of sites in Jordan with potentially high wind speeds to be utilized for producing electricity (Habali et al., 1987). Ras Munif, Mafraq and Aqaba are the three most potential wind sites in Jordan. Wind speed ranges from 4 to 23 m s-1 throughout 80% of the entire year. Wind electricity (Amr et al., 1993) could be utilized for sustaining human settlements and the habitat. In order to produce electricity from hydro-power it is suggested that seawater can be pumped during off- peak hours to an 8.2x106 m3 reservoir (Middle East Water Commission, 1995). This reservoir will be located at 600-650 m above sea level, in Aqaba mountain range. Water will be flown back to the sea through a penstock yielding an effective water pressure of 60 kg cm-2 at the end of the pipe. In addition to 100x106 m3 of fresh water, 600 MW of peak electric power can be produced annually (Middle East Water Commission, 1995; Akash et al., 1997). Nuclear electricity offers an advantage to diesel electricity from an environmental point of view. But nuclear power plants are highly capital intensive, it was reported that annual capital charges represent more than 70% of the total average annual production cost.
APPENDIX B
Real data concerning cost and benefit of the systems: Actual data as obtained from (National Electric Power Company in Jordan, 2005) for the costs of the five electricity generating systems are shown in Table B1 and the following two lists:
Auxiliary systems: The eight electricity generating systems are listed below based on the higher need of auxiliary systems:
| • | Wind and solar |
| • | Hydro |
| • | Diesel power generation systems and gas turbine |
| • | Nuclear |
| • | Fuel oil thermal power plants and oil shale |
Environmental constraints: The eight electricity generating systems are decently listed below based on environmental constraints:
| • | Wind, solar and hydro |
| • | Gas turbine |
| • | Diesel generation sets |
| • | Oil shale |
| • | Thermal power stations |
| • | Nuclear |
Actual data as obtained from (National Electric Power Company in Jordan, 2005) for the benefits of the eight electricity generating methods are shown in Table B2 below and the following three lists:
| Table B1: | Actual data for cost of the electricity generating systems in Jordan |
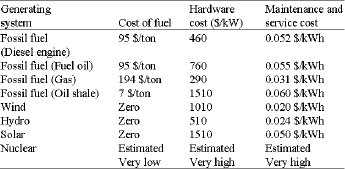 | |
| Table B2: | Actual data for benefit of the electricity generating systems in Jordan |
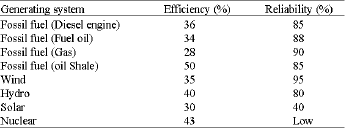 | |
National economy: The eight electricity generating methods are listed below based on their higher effect on the national economy:
| • | Hydro, wind and solar |
| • | Oil shale |
| • | Nuclear |
| • | Thermal power stations, diesel generation sets and gas turbine |
Social benefits and safety: The eight electricity generating systems are listed below based on their higher social benefits and safety:
| • | Wind, solar and hydro |
| • | Gas turbine |
| • | Diesel generation sets |
| • | Oil shale |
| • | Thermal power stations |
| • | Nuclear |
Availability of fuel: The eight electricity generating systems are listed below based on fuel availability:
| • | Oil shale |
| • | Wind and solar |
| • | Nuclear |
| • | Gas turbine |
| • | Hydro |
| • | Diesel generation sets and thermal power station |
REFERENCES
- Akash, B.A., R. Mamlook and M.S. Mohsen, 1999. Multi criteria selection of electric power plants using analytical hierarchy process. Electric Power Syst. Res. J., 52: 29-35.
CrossRef - Khalil, R.A.H., B.A. Jubran and N.M. Faqir, 1997. Optimization of solar pond for electrical power generation system. Energy Convers. Manage., 38: 787-798.
Direct Link - Kolb, G.J., 1998. Economic evaluation of solar only hybrid power towers using molten salt technology. Solar Energy, 62: 51-61.
Direct Link - Kribus, A., R. Zaibel, D. Carey, A. Segal and J. Karni, 1998. A solar driven combined cycle power plant. Solar Energy, 62: 121-129.
Direct Link - Mamlook, R., C. Tao and W.E. Thompson, 1999. An advanced fuzzy controller. Int. J. Fuzzy Sets Syst., 103: 541-545.
CrossRefDirect Link - Mamlook, R., B.A. Akash and M.S. Mohsen, 2001. A neuro fuzzy program approach for evaluating electric power generation systems. Energy, 26: 619-632.
Direct Link - Mamlook, R., B. Akash and S. Nijmeh, 2001. Fuzzy sets programming to perform evaluation of solar systems in Jordan. Energy Convers. Manage., 42: 1717-1726.
CrossRefDirect Link - Mamlook, R. and O.R.A. Jayyousi, 2003. Fuzzy sets analysis for leak detection in infrastructure systems a proposed methodology. Clean Technol. Environ. Policy J., 6: 26-31.
Direct Link - Murakami, M. and A.T. Wolf, 1995. Techno political water and energy development alternatives in the Dead Sea and Aqaba regions. Int. J. Water Res. Dev. 11: 163-184.
CrossRef - Oder, C., H.D. Haasis and O. Rentz, 2007. Analysis of the Lithuanian final energy consumption using fuzzy sets. Int. J. Energy Res., 17: 35-44.
Direct Link - Akash, B.A., O. R. Al-Jayyousi and M.S. Mohsen, 1997. Multi-criteria analysis of non-conventional energy technologies for water desalination in Jordan. Desalination, 114: 1-12.
CrossRefDirect Link








