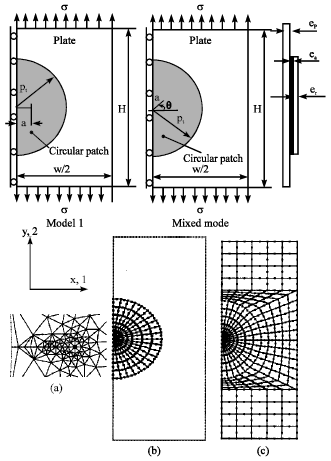
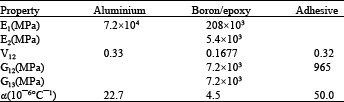
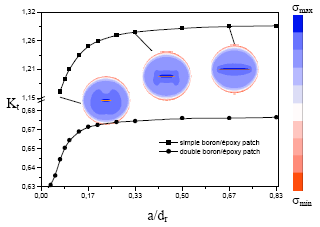
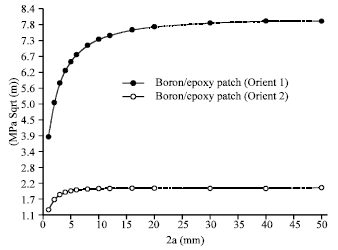
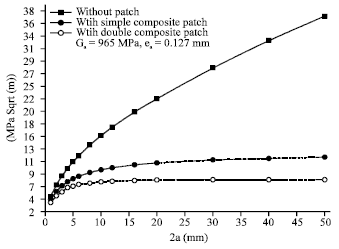
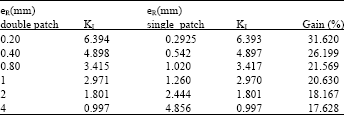
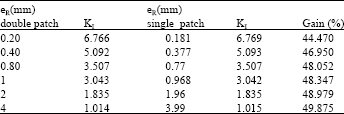
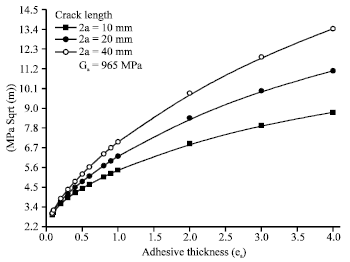
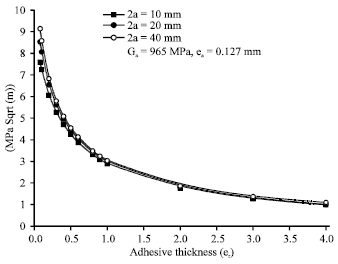
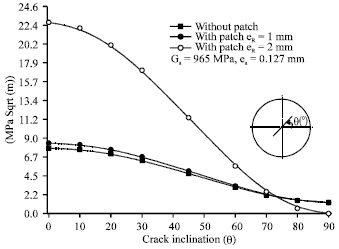
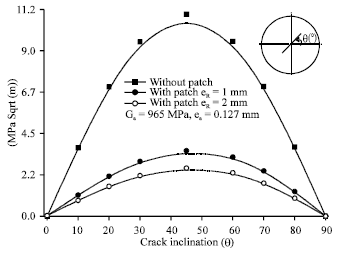
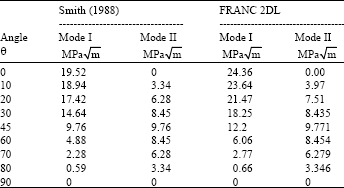
Research Article
Fracture Mechanics Modelling of Cracked Aluminium Panel Repaired with Bonded Composite Circular Patch
Department of mechanic, University Ibn Badis of Mostaganem-Algeria
A. Hebbar
Department of mechanic, University Ibn Badis of Mostaganem-Algeria
J. Vina Olay
Department of Material Sciences, University of Oviedo, 33204 Gij�n, Spain