ABSTRACT
The eigenvalue problems of annular plates are numerically formulated using the modified generalized differential quadrature method. The modified generalized differential quadrature method does not use the δ method. Appropriate boundary conditions accompany the modified generalized differential quadrature method to transform the partial differential equations of annular plates into discrete eigenvalue problems. Numerical results indicated that the accuracy of the calculated results is improved significantly by employing the modified generalized differential quadrature method. The effect of grid point number and the values of δ on the accuracy variation of calculated natural frequencies are also discussed.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2006.1591.1595
URL: https://scialert.net/abstract/?doi=jas.2006.1591.1595
INTRODUCTION
The concept of differential quadrature method introduced by Bellman and Casti (1971) and Bellman et al. (1972) has been used extensively to solve a variety of problems in different fields of science and engineering. The differential quadrature method has been shown to be a powerful contender in solving initial and boundary value problems and thus has become an alternative to the existing methods. Chen and Zhong (1997) pointed out that the differential quadrature method and the differential cubature method, due to their global domain property, are more efficient for nonlinear problems than the traditional numerical techniques such as finite element method and finite difference method. One of the fields among which can find extensive applications of the differential quadrature method is structural mechanics. Civan (1994) solved multivariable mathematical models using differential quadrature method and differential cubature method. Malik and Bert (1996) implemented the differential quadrature method multiple boundary conditions to free vibration of plates. In order to derive the weighting coefficients in a more explicit way, a generalized differential quadrature method was proposed by Quan and Chang (1989a, b). They presented that the generalized differential quadrature method is rather convenient in comparison with the differential quadrature method. Hua and Lam (1998) pointed out that generalized differential quadrature method is no restriction on the distribution and the number of discrete grid points used in the approximation process and the weighting coefficients are determined by using a simple recurrence relationship instead of by solving a set of linear algebraic equations. Dynamic characteristics of annular plates are of considerable importance in many designs. Azimi (1988a) solved free vibration of circular plates with elastic edge supports using the receptance method. Azimi (1988b) solved free vibration of circular plates with elastic or rigid interior support. Wang et al. (1995) studied free vibration analysis of circular annular plates with non-uniform thickness by the differential quadrature method. In this work, the generalized differential quadrature method is employed to formulate the discrete eigenvalue problems of annular plates. In the generalized differential quadrature method, two points, separated by a very small distance, δ are placed at each boundary point. If δ is used, the solution may show oscillation. δ influences the accuracy of the solution seriously. In this study a different approach is proposed for applications of the boundary conditions using the modified generalized differential quadrature method. The integrity and computational efficiency of the modified generalized differential quadrature method in this problem will be demonstrated through a series of case studies.
THE GENERALIZED DIFFERENTIAL QUADRATURE METHOD
For a function f(r), generalized differential quadrature method approximation for the m order derivative at the ith sampling point is given by
| (1) |
where N is the number of sampling points, ri the location of ith sampling points in the domain, f(ri) the functional values at these points and ![]() the weighting coefficients of m order differentiation attached to these functional values. The advantages of the generalized differential quadrature method over the differential quadrature method are that the general form of the test function is taken to be Lagrangian interpolation polynomial in order to determine the weighting coefficients
the weighting coefficients of m order differentiation attached to these functional values. The advantages of the generalized differential quadrature method over the differential quadrature method are that the general form of the test function is taken to be Lagrangian interpolation polynomial in order to determine the weighting coefficients ![]() instead of solving a set of linear algebraic equations. The test function is
instead of solving a set of linear algebraic equations. The test function is
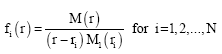 | (2) |
where
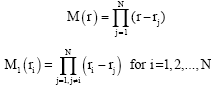 |
Other types of polynomials could be used as well. However, by using the Lagrangian interpolation polynomial, the numerical ill conditions in calculating the weighting matrix would be overcome. Introducing Eq. 2 into Eq. 1, one derives that
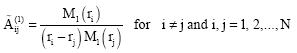 | (3) |
and
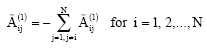 | (4) |
Once the sampling points are selected, the weighting matrix can easily be obtained from Eq. 3 and 4. For the second order and higher order derivatives, the weighting coefficients are obtained by using the following simple recurrence relation
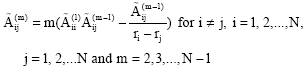 | (5) |
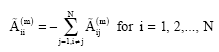 | (6) |
It is emphasized that the number of the test functions must be greater than the highest order of derivative in the governing equations.
CHOICE OF THE SAMPLING POINTS
The selection of locations of the sampling points plays a significant role in the accuracy of the solution of differential equations. For a domain separate into by N points, one could obtain equally spaced sampling points. Inner points are
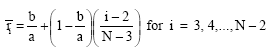 | (7) |
At each end, two points, separated from each other by a small distance δ, should be placed and boundary conditions applied at both points. Boundary points are
| (8) |
| (9) |
| (10) |
| (11) |
where, δ is small distance, b is the inner radius of the annular plate ![]() and a is the outer radius of the annular plate. Using equally spaced points can be considered to be a convenient and an easy selection method. For a domain separate into by N points, one could obtain a more accurate solution by choosing a set of unequally spaced sampling points. Bert and Malik (1996) pointed out simple and good choice can be the Chebyshev-Gauss-Lobatto points. Following nonuniform grid spacing gives better and more reliable results. Inner points are
and a is the outer radius of the annular plate. Using equally spaced points can be considered to be a convenient and an easy selection method. For a domain separate into by N points, one could obtain a more accurate solution by choosing a set of unequally spaced sampling points. Bert and Malik (1996) pointed out simple and good choice can be the Chebyshev-Gauss-Lobatto points. Following nonuniform grid spacing gives better and more reliable results. Inner points are
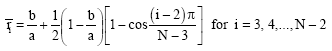 | (12) |
boundary points are
| (13) |
| (14) |
| (15) |
| (16) |
VIBRATION ANALYSIS
The axisymetric motion of an annular plate is governed by
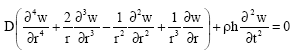 | (17) |
where, D is the flexural rigidity, h is the thickness of the annular plate, w = W sin(ωt), ω is the natural frequency of the annular plate, E is Young’s modulus of the material of the annular plate and ρ is the density of the material of the annular plate. Equation 17 can be transformed into the following equation
| (18) |
where,
At a clamped boundary, the transverse deflection of the plate is zero:
| (19) |
| (20) |
at a free boundary, the condition of zero normal moment can be reduced to
 | (21) |
The condition of zero effective shear force at a free boundary is given by
| (22) |
The generalized differential quadrature method is applied and Eq. 1 substituted into Eq. 18-22. Equations 18-22 can be rewritten as the following equations:
| (23) |
where,
| (24) |
| (25) |
| (26) |
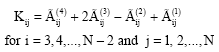 | (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
By solving the eigenvalue problem of Eq. 23, one will obtain the eigenvalues.
A DIFFERENT APPROACH FOR VARIOUS BOUNDARY CONDITIONS
If δ is too small, oscillation of solution may occur. In this study a different approach is proposed for application of the boundary conditions. The selection of locations of the sampling points plays a significant role in the accuracy of the solution of differential equations. For a domain separate into by N points, one could obtain unequally spaced sampling points. Inner points are
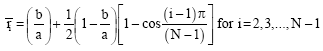 | (36) |
Different formulas are no two points at each of the ends and the boundary conditions applied at each of the points. Boundary points are
| (37) |
| (38) |
Equations 18-22 can be rewritten as the following equations:
| (39) |
where,
| (40) |
| (41) |
| (42) |
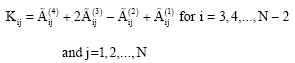 | (43) |
| (44) |
| (45) |
| (46) |
| (47) |
| (48) |
| (49) |
| (50) |
| (51) |
One will obtain the eigenvalues by solving the eigenvalue problem of Eq. 39. Computer programs are coded and developed in MATLAB to find the numerical results that are based on the modified generalized differential quadrature method.
RESULTS AND DISCUSSION
Figure 1 shows the non-dimensional frequencies ![]() of the clamped-free annular plate for b/a = 0.1. The present method gives the most accurate results for the fundamental frequency and shows good convergence. The numerical results solved using the modified generalized differential quadrature method show better than the results calculated using the generalized differential quadrature method. The numerical results are greatly improved using the modified generalized differential quadrature method. If δ is too small, the polynomial solution may show oscillations. One can observe that the present method renders very accurate numerical results even in the 7 sampling points case. One can numerically show convergence when the sampling points increase using the modified generalized differential quadrature method. Numerical results solved using the generalized differential quadrature method with, δ = 10-6, 5, 11, 13 and 24 sample points have ill conditions. Figure 2 plots the non-dimensional frequencies
of the clamped-free annular plate for b/a = 0.1. The present method gives the most accurate results for the fundamental frequency and shows good convergence. The numerical results solved using the modified generalized differential quadrature method show better than the results calculated using the generalized differential quadrature method. The numerical results are greatly improved using the modified generalized differential quadrature method. If δ is too small, the polynomial solution may show oscillations. One can observe that the present method renders very accurate numerical results even in the 7 sampling points case. One can numerically show convergence when the sampling points increase using the modified generalized differential quadrature method. Numerical results solved using the generalized differential quadrature method with, δ = 10-6, 5, 11, 13 and 24 sample points have ill conditions. Figure 2 plots the non-dimensional frequencies ![]() of the clamped-free annular plate for b/a = 0.2. The present method gives the most accurate results for the fundamental frequency and shows good convergence. The results solved using the present method show better than the results solved using the small distance δ for the clamped-free annular plates.
of the clamped-free annular plate for b/a = 0.2. The present method gives the most accurate results for the fundamental frequency and shows good convergence. The results solved using the present method show better than the results solved using the small distance δ for the clamped-free annular plates.
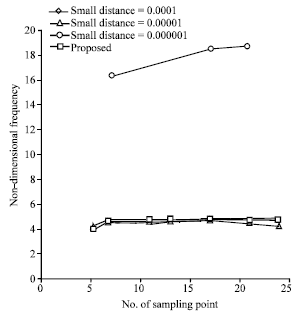 | |
| Fig. 1: | Non-dimensional frequencies |
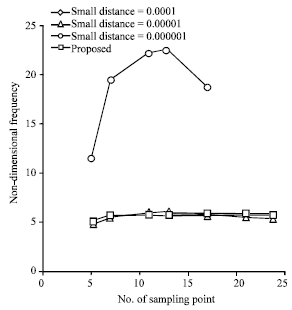 | |
| Fig. 2: | Non-dimensional frequencies |
One can observe that the present method presents very accurate numerical results even in the 7 sampling points case. One cannot numerically show convergence when the sampling points increase using the generalized differential quadrature method. Numerical results calculated using the generalized differential quadrature method with, δ = 10-6, 21 and 24 sample points have ill conditions.
CONCLUSIONS
In this study the modified generalized differential quadrature method is presented using a new differential quadrature formulation. A numerical solution for vibration of an annular plate is developed based on the implementation of modified generalized differential quadrature method. The results from several case studies validate the applicability of the method for solving such an engineering problem. The method provides accurate results with relatively minimal computational and modeling efforts. The modified generalized differential quadrature method did not use the δ method. It is concluded that the demonstrated accuracy and simplicity of the modified generalized differential quadrature method make it a good candidate for modeling more complicated cases of vibrations of annular plates. Results indicated that the modified generalized differential quadrature method accompanies appropriate boundary conditions is feasible and valid in formulating the eigenvalue problems of the annular plates.
REFERENCES
- Azimi, S., 1988. Free vibration of circular plates with elastic edge supports using the receptance method. J. Sound Vibration, 120: 19-35.
CrossRef - Azimi, S., 1988. Free vibration of circular plates with elastic or rigid interior support. J. Sound Vibration, 120: 37-52.
Direct Link - Bellman, R. and J. Casti, 1971. Differential quadrature and long-term integration. J. Math. Anal. Applic., 34: 235-238.
CrossRef - Bert, C.W. and M. Malik, 1996. Differential quadrature method in computational mechanics: A review. Applied Mech. Rev., 49: 1-28.
CrossRef - Malik, M. and C.W. Bert, 1996. Implementing multiple boundary conditions in the DQ solution of higher-order PDEs: Application to free vibration of plates. Int. J. Numer. Methods Eng., 39: 1237-1258.
CrossRefDirect Link








