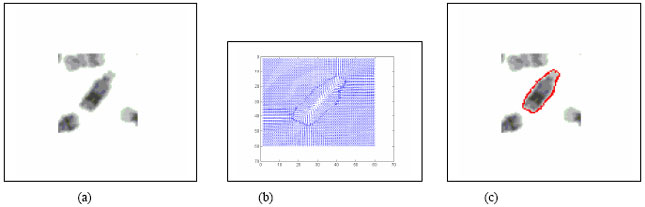
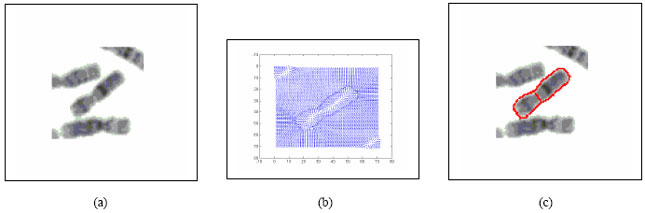
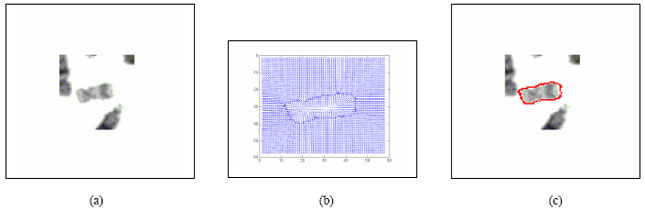
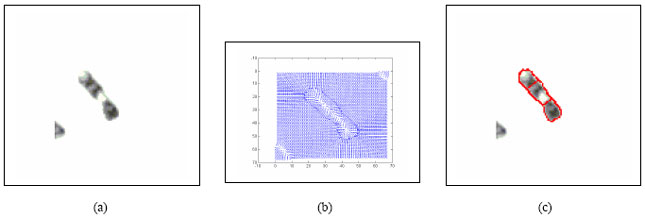
Research Article
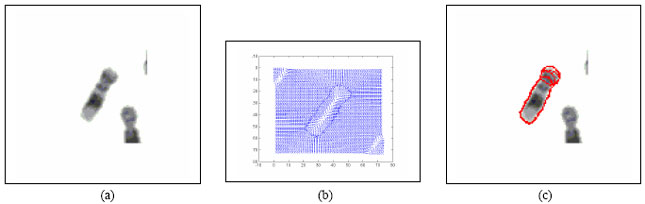
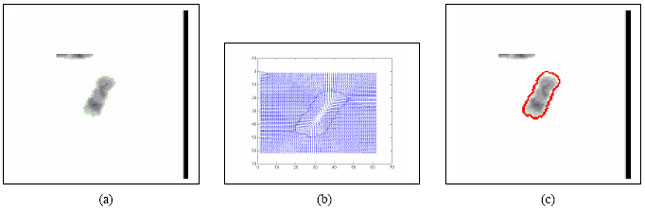
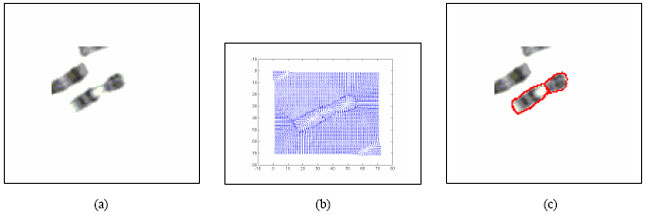
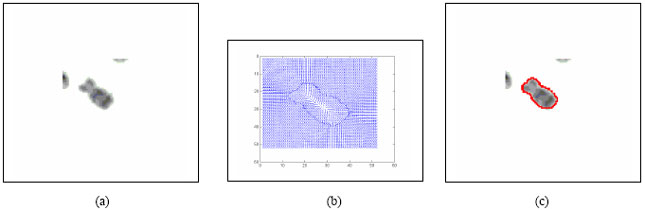
Boundary Mapping of Chromosome Spread Images Using Optimal Set of Parameter Values in Discrete Cosine Transform Based Gradient Vector Flow Active Contours
Center for Medical Electronics, Department of Electronics and Communication Engineering, India
G. Ravindran
Faculty of Information and Communication Engineering, Anna University, Chennai, India