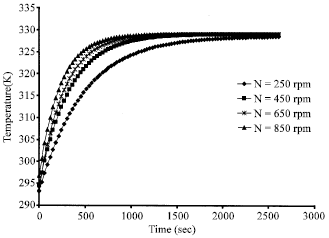
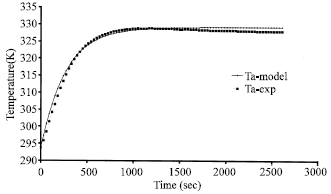
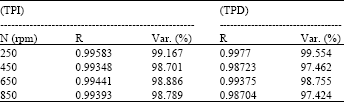
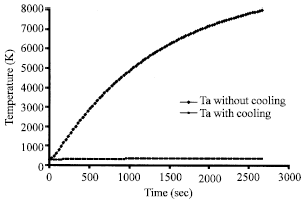
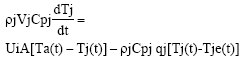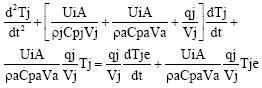Research Article
Modeling and Simulation of Thermal Transfer in Batch Reactor
Department of Chemistry, Faculty of Science, University of Sciences and Technology of Oran, BP 1505 EL Mnouar, Oran, Algeria
M. Benyettou
Laboratory of Modeling and Optimization of Industrial Systems, Faculty of Science, University of Sciences and Technology of Oran, BP 1505 EL Mnouar, Oran, Algeria