Research Article
Implementation of s-stage Implicit Runge-Kutta Method of Order 2s for Second Order Initial Value Problems
Department of Computer Science, Faculty of Applied Sciences, International Islamic University, Sector H-l O, Islamabad, Pakistan
Khalid Rashid
Department of Computer Science, Faculty of Applied Sciences, International Islamic University, Sector H-l O, Islamabad, Pakistan









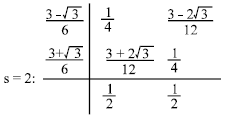
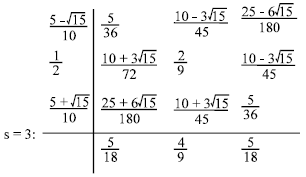
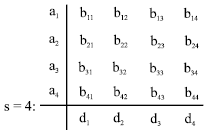
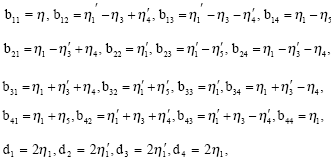
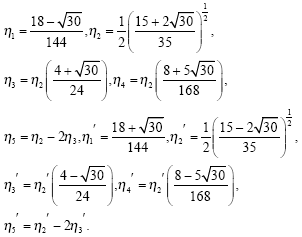
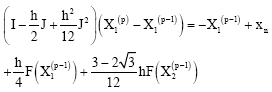
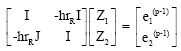
 gives
gives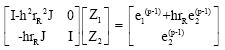
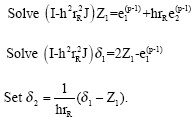

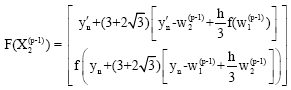
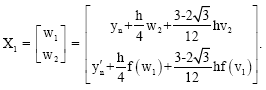
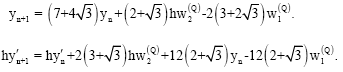
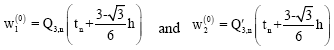
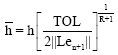

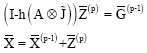

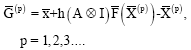
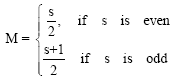
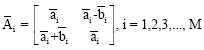
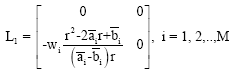
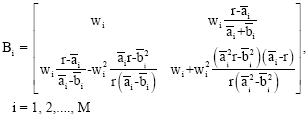



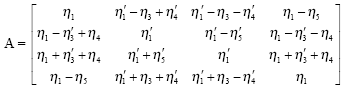
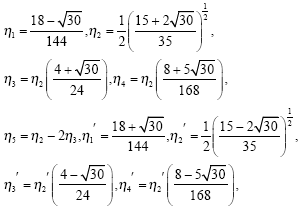
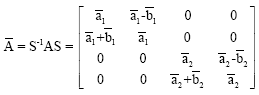
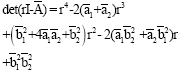

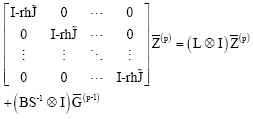
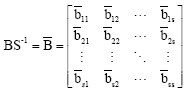
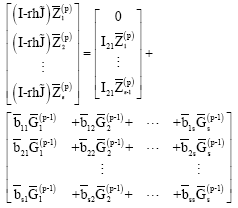
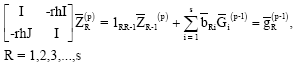
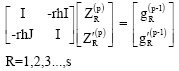
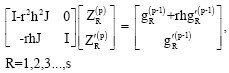

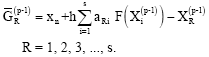
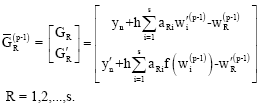
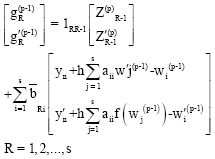
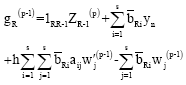
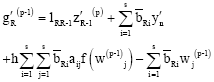
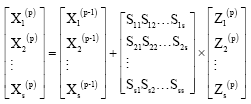
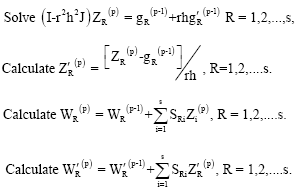
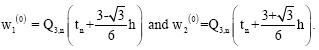 This predictor cannot be used on the first step and so on this step, we propose to use
This predictor cannot be used on the first step and so on this step, we propose to use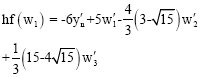
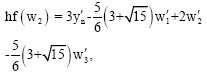
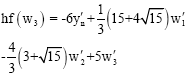
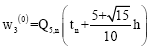 However this predictor cannot be used on the first two steps. Instead, on the first step, we propose to use
However this predictor cannot be used on the first two steps. Instead, on the first step, we propose to use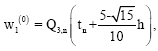

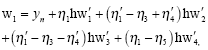
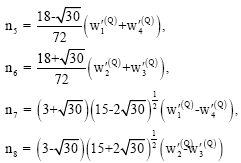
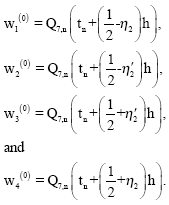
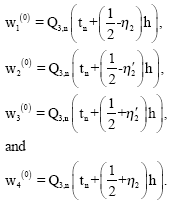
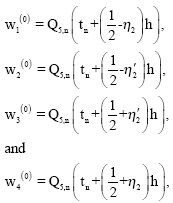
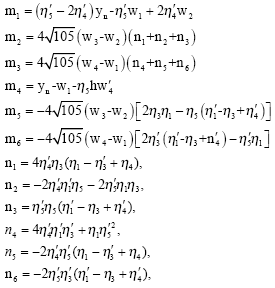
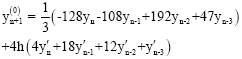












Aminu Mustafa Reply
Was fortunate to have the paper.The paper is well explained with details Examples and simple grammar.