Research Article
Modeling of Daily Pan Evaporation
Faculty of Technical Education, Suleyman Demirel University, Isparta 32260, Turkey
M. Erol Keskin
Faculty of Engineering-Architecture, Suleyman Demirel Umversity, Isparta 32260, Turkey
Evaporation is the necessary components in any water balance assessments for different water resources planning, design, operation and management studies including hydrology, agronomy, forestry and land resources, irrigation management, river flow forecasting, investigation of lake ecosystem and modeling, etc. Among the components of the hydrological cycle, evaporation is perhaps the most difficult to estimate owing to complex interactions between the components of the land-plant-atmosphere system[1]. This is further true for lakes such as in the eastern province of Turkey where naked land-water-mountain composition gives difficulties for detailed evaporation measurement records for long time periods. It is therefore necessary to develop approaches to estimate the evaporation rates from other available meteorology variables, which are comparatively easier for measurements. There are many available direct and indirect methods but it is always preferable to have evaporation measurements simultaneously with other relevant meteorological variables for the development of an effective evaporation model to estimate evaporation. The class A pan and eddy correlation are among the direct methods[2]. Indirect methods include those that use meteorological data to estimate evaporation from other meteorological variables through empirically developed methodologies or statistical and stochastic approaches in addition to mass-balance based formulations. Both direct and indirect methods have been used for evaporation estimation studies by many researchers[3-8].
One of the recent digressions from the classically available approaches is the Artificial Neural Networks (ANN), which provides better modeling flexibility than the previous approaches with its successive adaptive features of error propagation where each meteorological variable takes its share proportionately. Numerous researchers have shown applicability of artificial neural networks in hydrological practices. For instance, solar radiation has been estimated using radial basis function and multilayer perceptron ANN[9]. They have used latitude, longitude, altitude, sunshine hours and the month of the year as inputs in order to estimate the solar irradiation. The comparison of the model results to observed values indicates that the ANN with radial basis function provides satisfactory estimations. Tasadduq et al.[10] have developed an ANN model for hourly mean ambient temperature prediction 24 h in advance. The comparison of predictions with the actual measurements favored the use ANN architecture in such prediction affairs, which encourages the use of ANN in hourly meteorological predictions. On the other hand, ANN models have also been used by many researchers to estimate short-term streamflow from meteorological variables in order to depict the rainfall-runoff relationship[11-19].
The main aim of this study was to develop a suitable ANN model by considering the feed-forward back-propagation learning algorithm in the estimation of daily pan evaporation.
ARTIFICIAL NEURAL NETWORKS (ANNs)
Neural networks are composed of simple elements operating in parallel. These elements are inspired by biological nervous systems. As in nature, the network function is determined largely by the connections between elements. A neural network can be trained to perform a particular function by adjusting the values of the connections (weights) between the elements. Commonly neural networks are adjusted, or trained, so that a particular input leads to a specific target output[20].
Feed forward ANNs comprise a system of neurons, which are arranged in successive layers, namely input and output layers in addition to one or more hidden layers. The neurons in each layer are connected to the neurons in the subsequent layer by a weight w, which may be adjusted during training. A data pattern comprising the values xi presented at the input layer i is propagated forward through the network towards the first hidden layer j. Each hidden neuron receives the weighted outputs wjixi from the neurons in the previous layer. These are summed to produce a net value (NETj), which is then transformed to an output value upon the application of an activation function[11].
A typical three-layer feed-forward ANN is showed in Fig. 1. A typical ANN consists of three layers, namely input, hidden and output layers. Input layer neurons are xo, x1, x2… xn; hidden layer neurons are h1, h2… hn; and finally output layer neurons are o1, o2… on.
A neuron consists of multiple inputs and a single output. The sum of the inputs and their weights lead to a summation operation as,
| (1) |
in which wij is established weight, xij is input value and NETj is input to a node in layer j.
The output of a neuron is decided by an activation function. There are a number of activation functions that can be used in ANNs such as step, sigmoid, threshold, linear etc. The logistic sigmoid function, f(x), commonly used, can be formulated mathematically as:
| (2) |
| (3) |
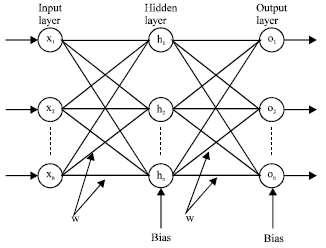 | |
| Fig. 1: | A typical three-layer feed-forward ANN |
The back-propagation learning algorithm is applied to multilayer feed-forward networks consisting of processing elements with continuous and differentiable activation functions. Given a training set of input-output pairs, the algorithm provides a procedure for changing the weights in a back-propagation learning algorithm to classify the given input patterns correctly. The basis for this weight update algorithm is simply the gradient-descent method as used for simple perceptrons with differentiable neurons.
For a given input-output pair, the back propagation algorithm performs two phases of data flow. First, the input pattern is propagated from the input layer to the output layer and, as a result of this forward flow of data, it produces an actual output. Then the error signals resulting from the difference between output pattern and an actual output are back-propagated from the output layer to the previous layers for them to update their weights[21].
Study region and data: Lake Egirdir (lat. 37.80° and 38.43°N, lon.30.30° and 31.37°E) is a freshwater lake located in Lakes District of Turkey which is the second largest freshwater lake in the country with a surface area and volume as 470 km2 and 4360 hm3, respectively. It is being used as water supply and irrigation purposes. This Lake is of tectonic origin in the northern part of the Egirdir County. The altitude of the lake is about 916 m above mean sea level. Geographically, the lake lies on a 50 km stretch on the north-south direction. The distance between east and west shores is 3 km, at which the depth is around 1.8 m. The mean depth of the lake is 8 to 9 m and the deepest point is 15 m. In the southern part, the width of the lake reaches a maximum of 16 km.
Meteorological data for ANN model were obtained from an Automated GroWeather Meteorological Station near Lake Egirdir. Meteorological parameters included air and water temperature, relative humidity, solar radiation, wind speed and air pressure were logged. Class A pan evaporation values used as output in the ANN models are measured daily by XVIII. District Directorate of State Hydraulic Works. The data used to develop ANN models included 490 daily observations from March 1 to October 31, 2001 and 2002 years.
ANN EVAPORATION MODELS
Scatter diagrams are plotted between daily pan evaporation values and measured meteorological parameters in order to determine the dominating factors affecting evaporation in the lake location. Consideration of correlation coefficients indicates that the dominating factors affecting evaporation are their order of significance, air temperature (Ta), water temperature (Tw), solar radiation (RC), air pressure (Pa), relative humidity (Rh) and wind speed (U2). The Rh and U2 parameters with the least effects are neglected in ANN evaporation model architecture. In order to estimate daily pan evaporation from Lake Egirdir, ANN evaporation models with two (Ta and Tw), three (Ta, Tw and RC) and four input variables (Ta, Tw, RC and Pa) are considered.
The adequacy of the ANN evaporation models was evaluated by estimating the coefficient of determination (R2) defined based on the evaporation estimation errors as:
| (4) |
where:
| (5) |
| (6) |
where, Ei(Pan) and Ei(simulated) are daily pan measurement and ANN model evaporation estimation values, respectively with the mean daily pan evaporation, Emean. The Mean Square Error (MSE) is defined as
| (7) |
and used in order to decide about the best model, where n is the number of observed data.
In this study, ANN(i,j,k) indicates a network architecture with I, j and k neurons in input, hidden and output layers, respectively. Herein, i runs from 2, 3, to 4; j assume values of 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 where as k = 1 is adopted in order to decide about the best ANN model alternative. Prior to execution of the model, standardization of the data, Xi, (i = 1, 2, …,n) is done according to the following expression such that all data values fall between 0 and 1.
| (8) |
where, xi is the standardized value but Xmax and Xmin are the maximum and minimum measurement values. Such standardization procedures renders the data also into dimensionless form.
An alternative model selection method, which is often employed in the ANN is the cross-validation. It does not remove the uncertainty completely by cross-validation. The motivation for this model selection is similar to the line of arguments leading to information criteria. Model complexity does not result necessarily in a better description of the underlying function due to increasing estimation error. In order to find an appropriate degree of complexity, it is appealing to compare the MSE of different model specifications. Such prediction errors are obtained by sampling the data into M subsets (M = 5 in the study), with n observations each. From the M available sets of observed data, (M-1) are used to train the ANN. After the training is finished, the data set left out is predicted and the result is compared to the observed data. This procedure is repeated M times, once for each training data set. The average MSE on the M subsets that have been left out defines the cross-validation error. If, for instance, a large value of this error is obtained, the point excluded during the training process is important and its absence will produce an ANN with poor estimation and generalization capabilities. On the other hand, if the associated error is small, it means that the data set has enough support from its neighbors that its presence is not very important[22,23].
For ANN models the number of hidden layers considered after trial and cross-validation is only one in all the structures proposed and the numbers of hidden neurons are obtained 5, 6 and 3. These structures are represented by ANN(2,5,1), ANN(3,6,1) and ANN(4,3,1), respectively. The learning rate and momentum parameters affect the speed of the convergence of the back-propagation algorithm.
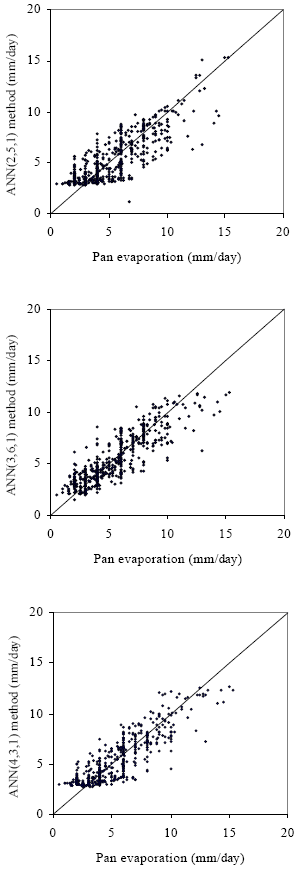 | |
| Fig. 2: | Comparison daily pan evaporation with ANN(2,5,1), ANN(3,6,1) and ANN(4,3,1) models |
A learning rate of 0.001 and momentum 0.1 are fixed for selected network after training and model selection is completed for year 2001.
| Table 1: | R2 and MSE values between ANN models and daily pan evaporation |
 | |
The trained networks are used to run a set of test data for year 2002. The performance indices reveal that the ANN(4,3,1) model is superior among ANN models. Comparing the performance of the ANN(4,3,1) and ANN(3,6,1) models, it can be observed that these models are performed in a more similar way. The difference between these two models is only in the input variables. The ANN(3,6,1) model depends on daily mean values of air temperature, water temperature and solar radiation, but ANN(4,3,1) is based on air pressure of three parameters. ANN(4,3,1) has better R2 and lower MSE than ANN(3,6,1) model for both training and testing as shown in Table 1.
The performance of ANN(4,3,1) model suggests that the evaporation could be estimated easily from available data using ANN approach. The results of ANN models are plotted against measured daily pan evaporation in Fig. 2. ANN(4,3,1) model comparison plot is also around 45° straight lines which imply that there are no bias effects in the model. Therefore, ANN(4,3,1) is selected for daily pan evaporation estimation in this study. Formulations of ANN(4,3,1) model can be written as follows:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
in which Ta: air temperature (°C), Tw : water temperature (°C), RC : solar radiation (cal/cm2/day), Pa : air pressure (kPa), E : evaporation (mm/day), NET1-NET4 and F1-F3 equations are summation and activation function of each neuron at hidden layer, respectively. Although these equations are obtained for Lake Eğirdir, it can be also adapted for various locations.
Estimating evaporation is important in hydrological practices. There are many available direct and indirect methods used to estimate evaporation. In addition to these methods, alternative model was proposed herein to estimate evaporation using ANN model. Comparing ANN models, ANN(4,3,1) model is superior among ANN models. The comparison shows that there is a better agreement between the results of ANN(4,3,1) model and pan evaporation values than others model. The evaporation could be estimated easily from available data using ANN approach. ANN model can be adapted to estimate, not to measure, daily pan evaporation for Lake Egirdir where it is either not measured or the measurement system has failed. ANN model formulations can be developed changing input variables to estimate evaporation values in various location.