ABSTRACT
In this study, Gene Expression Programming (GEP) is used in modeling the deflection basins measured on the surface of the flexible pavements. Backcalculation of the pavement layer moduli are well-accepted procedures for the evaluation of the structural capacity of pavements. The ultimate aim of the backcalculation process from Nondestructive Testing (NDT) results is to estimate the pavement material properties. Using backcalculation analysis, in situ material properties can be backcalculated from the measured field data through appropriate analysis techniques. In order to backcalculate reliable moduli, deflection basin must be realistically modeled. In this study, GEP was used to model the deflection basin characteristics. Experimental deflection data groups from NDT are used to show the capability of the GEP approach in modeling the deflection bowl. This approach can be easily and realistically performed to solve the problems which do not have a formulation or function about the solution.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.309.314
URL: https://scialert.net/abstract/?doi=jas.2005.309.314
INTRODUCTION
Nondestructive Testing (NDT) and backcalculating pavement layer moduli are well-accepted procedures for the evaluation of the structural capacity of pavements[1]. NDT enables the use of a mechanistic approach for pavement design and rehabilitation because in situ material properties can be backcalculated from the measured field data through appropriate analysis techniques[2]. In order to backcalculate reliable moduli, it is essential to accomplish several deflection tests at different locations along the highway sections having the same layer thicknesses[1]. However, this is not enough to backcalculate pavement layer moduli. If and only if deflection basin is realistically modeled, elastic pavement layer moduli obtained from backcalculation results will reflect actual behavior of the pavement. In deflection methods, commercially available devices are the Dynaflect, Road Rater and Falling Weight Deflectometer (FWD). The most common property found by NDT is the elastic modulus of each pavement layer.
In recent years, one of the most important and promising research field has been “Heuristics from Nature”, an area utilizing some analogies with natural or social systems and using them to derive non-deterministic heuristic methods and to obtain very good results. Genetic Algorithms (GA) is one of the heuristic methods[3].
Everybody agrees that, by and large, evolution relies on genetic variation coupled with some kind of selection and, in fact, all evolutionary algorithms explore these fundamental processes. In all evolutionary algorithms, an evolutionary epoch or run starts with an initial population. Initial populations, though, are generated in many different ways and the performance and the costs (in terms of CPU time) of different algorithms depend greatly on the characteristics of initial populations. The simplest and less time consuming population is the totally random initial population. However, few evolutionary algorithms are able to use this kind of initial population due not only to structural constraints but also to the kind of genetic operators available to create genetic modification. The initial populations of Gene Expression Programming (GEP) are totally random and consist of the linear genomes of the individuals of the population[4].
GEP is a genotype/phenotype system that evolves computer programs of different sizes and shapes (expression trees) encoded in linear chromosomes of fixed length. The genetic encoding used in GEP allows a totally unconstrained interplay between chromosomes and expression trees. This interplay brought about a tremendous increase in performance allowing, consequently, the undertaking of detailed, much needed analysis of fundamental evolutionary processes.
In GEP, due to the existence of a truly functional and autonomous genome, the implementation of different genetic operators is extremely simplified Furthermore, due to the high efficiency of the algorithm, the performance and the roles of all these operators can be easily and rigorously analyzed revealing the existence of two fundamental types of evolutionary dynamics: non-homogenizing dynamics found in populations undergoing mutation or other non-conservative operators and homogenizing dynamics found in populations undergoing re-combination alone. Therefore, systems with different evolutionary behaviors can be easily simulated in GEP. In this study, the importance of the initial diversity is analyzed in two different systems. The first evolves under mutation and has a non-homogenizing dynamics characteristic of an efficient adaptation. The second evolves under recombination and has a homogenizing dynamics characteristic of poorly evolving systems[5].
Backcalculation of pavement layer moduli: Highway and transportation agencies have an increased responsibility for maintenance, rehabilitation on management of highways, particularly with regard to asphaltic concrete pavements. Efficient and economical methods are required to determine the structural properties of existing pavements realistically from non-destructive test data. This kind of evaluation is one of the most efficient and economical methods and has been increasingly used in the pavement engineering community. Pavement structural properties may be generally stated in terms of resilient modulus which is a key element in mechanistic pavement analysis and evaluation procedures.
Backcalculation generally refers to an iterative procedure whereby the layer properties of the pavement model are adjusted until the computed deflections under a given load agree with the corresponding measured values. NDT and backcalculating pavement layer moduli are well-accepted procedures for the evaluating of the structural capacity of pavements. NDT is meant to produce numerous deflection bowls. The ultimate aim of the backcalculation process from NDT results is to estimate the pavement material properties. The backcalculation procedure is to find the set of parameters corresponding to the best fit of the measured deflection bowls. Even if the deflections are measured accurately, backcalculation process does not give accurate results unless the backcalculation procedure is realistic.
FWD delivers a load to a pavement surface; then deflections are measured at several points of observation around the load. If layer elastic moduli are found so that the analytic deflections nearly coincide with measured deflections, the set of elastic moduli may be considered to represent average elastic moduli of real pavement structure. So far, Least Squares Method (LSM) was used for modeling both computed and measured deflection basin in backcalculation procedures. However, it can be said that LSM does not accurately model the deflection bowl. If the deflection basin is modeled as realistic as possible, then pavement layer moduli values obtained from backcalculation will give more realistic results. More precision is needed from the backcalculation procedures and more realistic models will reduce the size of systematic errors[6,7]. This will make it possible to predict the remaining life of a pavement realistically in the field immediately after it has been tested. For this reason, in this work, deflection basin was modeled using GA technique as a realistic approach.
FWD testing device: In order to simulate the truck loading on the pavement, a circular plate is dropped on the pavement from a certain height. The height is adjusted according to the desired load level. Underneath the circular plate a rubber pad is mounted to prevent the shock loading. Seven geophones are generally mounted on the trailer (the number of geophones can change). When the vertical load is applied on the pavement, the geophones collect the data in a byte form. Using the calibration factors, the bytes can be converted to the real deflections.
The FWD is a trailer mounted device which applies a load to the pavement surface through a circular plate. FWD testing has been established world-wide as one of the most effective tools for measuring deflections for pavement evaluation purposes[8]. Benkelman Beam and Dynaflect which are other mostly used devices in the developing countries only give the information about underneath the circular plate whereas the FWD gives the information about other six points which are away from the circular plate. Hence, the effect of the wheel loading can also be seen in other points when FWD is used.
There are many types of FWDs which can apply the same loading. The frequencies of loading change between 0.025 and 0.030 sec; the applied loads vary between 6.7-156 kN. The loads are generally applied in a sinusoidal form[9-11]. The loading time of 0.030 sec represents the wheel loading moving at a speed of 30 km h-1 and ±0.023 mm deviations can be seen from the FWD measurements[12]. A crew can be carried out 200-300 FWD measurements in a day.
Genetic algorithms: The fundamental unit of information is in living systems in the gene. In general, a gene is defined as a portion of a chromosome that determines or affects a single character or phenotype (visible property), for example, eye colour. It comprises a segment of Deoxyribonucleic Acid (DNA), commonly packaged into structures called chromosomes.
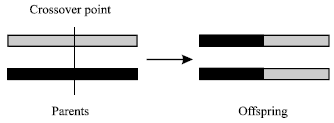 | |
| Fig. 1: | Example of one-point crossover |
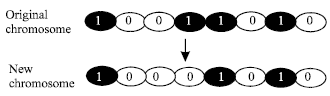 | |
| Fig. 2: | Bit mutation on the fourth bit |
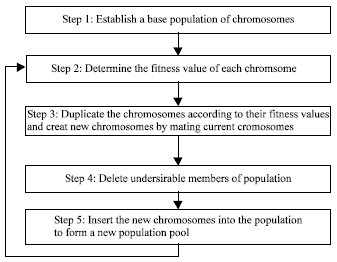 | |
| Fig. 3: | Basic steps of genetic algorithm[15] |
This genetic information is capable of producing a functional product which is most a protein[13].
Genetic Algorithm (GA) is inspired by the mechanism of natural selection where stronger individuals are likely the winners in a competing environment. Here, GA uses a direct analogy of such natural evolution. Through the genetic evolution method, an optimal solution can be found and represented by the final winner of the genetic game[13].
GA presumes that the potential of ant problem is an individual and can be represented by set of parameters. These parameters are regarded as the genes of a chromosome and can be structured by a string of values in binary form. A positive value, generally known as a fitness value, is used to reflect the degree o “goodness” of chromosome for the problem which would be highly related with its objective value[13].
Throughout a genetic evolution, the fitter chromosome has a tendency to yield good quality offspring which means a better solution to any problem. In a practical GA application, a population pool of chromosomes has to be installed and these can be randomly set initially. In each cycle of genetic operation, termed as an evolving process, a subsequent generation is created from the chromosomes, generally called “parents” or a collection term “mating pool” is selected via a specific selection routine. The genes of the parents are mixed and recombined for the production of offspring in the next generation. It is expected that from this process of evolution (manipulation of genes), the “better” chromosome will create a larger number of offspring and thus has a higher chance of surviving in the subsequent generation, emulating the survival-of-the-fittest mechanism[13].
A scheme called Roulette Wheel Selection is one of the most common techniques being used for such a proportionate selection mechanism. The cycle of evolution is repeated until a desired termination criterion is reached. This criterion can also be set by the number of evolution cycles (computational runs), or the amount of variation of individuals between different generations, or a pre-defined value of fitness[13].
In order to facilitate the GA evolution cycle, two fundamental operators: Crossover and mutation are required, although the selection routine can be termed as the other operator. To further illustrate the operational procedure, a one-point crossover mechanism is depicted on Fig. 1. A crossover point is randomly set. The portions of the two chromosomes beyond this cut-off point to the right are to be exchanged to form the offspring. An operation ret with a typical value between 0.6 and 1.0 is normally used as the probability of crossover[13].
However, for mutation (Fig. 2), this applied to each offspring individually after the crossover exercise. It alters each bit randomly with a small probability with a typical value of less than 0.1[13].
Living organisms are consummate problem solvers. They exhibit a versatility that puts the best computer program to shame. This observation is especially galling for computer scientist, who may spend months or years of intellectual effort on an algorithm, whereas organisms come by their abilities through the apparently undirected mechanism of evolution and natural selection.
Pragmatic researchers see evolution’s remarkable power as something to be emulated rather than envied. Natural selection eliminates one of the greatest hurdles in software design: specifying in advance all the features of a problem and the actions a program should take the deal with them.
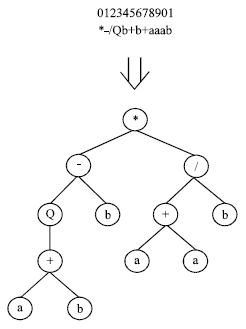 | |
| Fig. 4: | An example of ETs |
 | |
| Fig. 5: | An example of Karva language |
By harnessing the mechanism of evolution, researchers may able to “breed” programs that solve problems even when no person can fully understand their structure. Indeed, these so-called genetic algorithms have already demonstrated the ability to make breakthroughs in the design of such complex systems as jet engines[14].
Genetic algorithms make it possible to explore a far greater range of potential solutions to a problem than do conventional programs. Furthermore, as researchers probe the natural selection of programs under controlled and well-understood conditions, the practical results they achieve may yield some insight into the details of how life and intelligence evolved in natural world[14].
Basic steps of genetic algorithms: Given a way or a method of encoding solution of a problem into the form of chromosomes and given an evaluation function that returns a measurement of the cost value of any chromosome in the context of the problem, a GA consist of the following steps (Fig. 3)[15].
| Step 1: | Initialize a population of chromosomes. |
| Step 2: | Evaluate each chromosome in the population. |
| Step 3: | Create new chromosomes by mating current chromosomes; apply mutation and recombination as the parent chromosomes mate. |
| Step 4: | Delete members of population to make room for new chromosomes. |
| Step 5: | Evaluate the new chromosomes and insert them into the population. |
| Step 6: | If stopping criterion is satisfied, then stop and return the best chromosome; otherwise, go to step 3. |
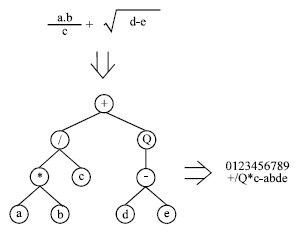
Gene expression programming: The phenotype of GEP individuals consists of the same kind of ramified structures used in genetic programming. However, these complex entities are encoded in simpler, linear structures of fixed length – the chromosomes. Thus, there are two main players in GEP: the chromosomes and the ramified structures or expression trees (ETs), the latter being the expression of the genetic information encoded in the former. Figure 4 shows an example of ETs.
As in nature, the process of information decoding is called translation.. And this translation implies obviously a kind of code and a set of rules. The genetic code is very simple: a one-to-one relationship between the symbols of the chromosome and the functions or terminals they represent. The rules are also very simple: they determine the spatial organization of the functions and terminals in the ETs and the type of interaction between sub-ETs in multi-genic systems. In GEP there are therefore two languages: the language of the genes and the language of ETs. However, thanks to the simple rules that determine the structure of ETs and their interactions, it is possible to infer immediately the phenotype given the sequence of a gene and vice versa. This bilingual and unequivocal system is called Karva language. Figure 5 shows an example of Karva language[16].
| Table 1: | Structure of the model |
 | |
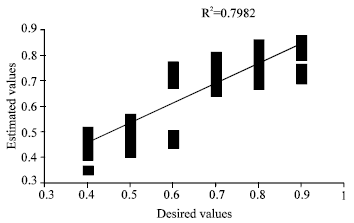 | |
| Fig. 6: | Regression curve of training set |
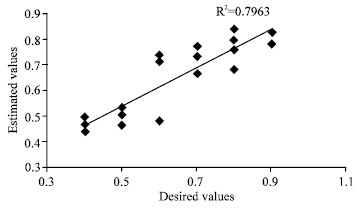 | |
| Fig. 7: | Regression curve of test set |
Modeling with gene expression programming: In order to model the deflection basin, seven deflection measurement points were used as input. Ninety five data sets are used for training and 19 data sets are used for testing. Table 1 shows the structure of the used model.
At the end of 10000 generation, best fitness was found as 772.8. Figure 6 and 7 show the regression curves of the model.
The formula obtained from GEP is shown in Eq. 1.
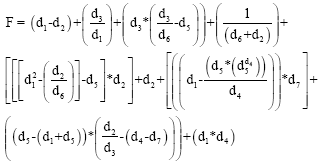 | (1) |
where, F is surface layer thickness; di is the deflection value in sensor I.
CONCLUSIONS
Modeling the deflection basin is very important in backcalculating flexible pavement layer moduli. In this work, a model for the deflection basins measured on the surface of the flexible pavements has been presented. The GEP approach was applied to model deflection basins. GEP is especially appropriate for investigating the complex deflection basin forms in evaluating the structural capacity of the flexible pavements. GEP application has been introduced through an example on deflection basins measured on the surface of a flexible pavement.
This new methodology can help the highway agency for estimating deflection basin in backcalculation process of flexible pavement layer moduli.
Some models formed in solution of a number of problems are based on assumptions and cannot reflect the reality. Solutions of the optimization problems which do not have a formulation or function about the solution can be easily and realistically performed using approach presented here.
REFERENCES
- Uzan, J., R.L. Lytton and F.P. Germann, 1989. General Procedure for Backcalculating Layer Moduli. In: Nondestructive Testing of Pavements and Backcalculation of Moduli, STP1026, Bush, A.J. and G.Y. Baladi (Eds.). American Society for Testing and Materials, Philadelphia, ISBN: 0803112602, pp: 217-227.
- Chow, T.T., G.Q. Zhang, Z.L. Lin and C.L. Song, 2002. Global optimization of absorption chiller system by genetic algorithm and neural network. Energy Build., 34: 103-109.
Direct Link - Saltan, M. and S. Terzi, 2004. Backcalculation of pavement layer parameters using artificial neural networks. Indian J. Eng. Mater. Sci., 11: 38-42.
Direct Link - Saltan, S., 2002. Modeling deflection basin using neurofuzzy in backcaluculating flexible pavement layer moduli. Inform. Technol. J., 1: 180-187.
CrossRefDirect Link - Ferreira, C., 2002. Gene Expression Programming in Problem Solving. In: Soft Computing and Industry-recent Applications, Roy, R., S. Ovaska, T. Furuhashi and F. Hoffman (Eds.). Springer-Verlag, Uk, pp: 635-654.
CrossRefDirect Link - Terzi, S., M. Saltan and T. Yildirim, 2003. Optimization of the deflection basin by genetic algorithm and neural network approach. Proceedings of the ICANN/ICONIP Joint International Conference on Artificial Neural Networks and Neural Information Processing, Junuary 26-29, 2003, Istanbul, Turkey, pp: 179-179.
CrossRef








