Research Article
Predicting the Crack Initiation Fracture Toughness for a Crack along the Bimaterial Interface
Department of Manufacturing and Materials Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
M. Azram
Department of Science in Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
M.H. Iliyas
Department of Manufacturing and Materials Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia











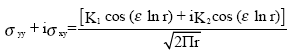



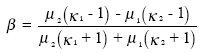
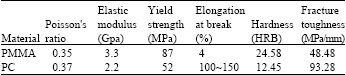
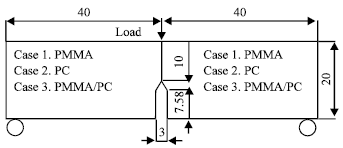
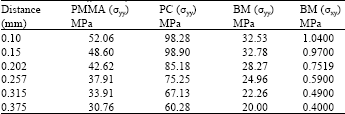
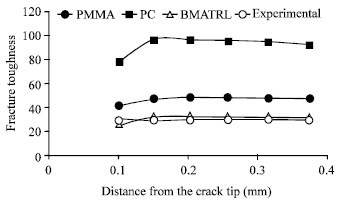
 for plane stress, while
for plane stress, while