ABSTRACT
In this study, the uncertainties of the optical basicity calculation based on the optical band gap and the refractive index for two glass systems (K2O-Nb2O5-TeO2, B2O3-Na2O-TeO2), have been estimated. The results benefits are very important in the determination of the optical basicity of binary and ternary glass systems. It has been established that as in the binary glass systems, there is a general trend of increasing the oxide ion polarizability with decreasing the oxide optical band gap and increasing the refractive index of the glass samples. Also it has been found that the uncertainty of the optical basicity estimation is around ±5 to ±15%. Some tables have been reported to help us predict the method used to determine the optical basicity for a glass system accurately.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.1867.1870
URL: https://scialert.net/abstract/?doi=jas.2005.1867.1870
INTRODUCTION
Optical basicity was proposed by Duffy and Ingram[1,2] is used as a measure of acid- base properties of oxides and glasses. Dimitrov and Sakka[3] have estimated the optical basicity of many simple oxides on the bases of the average oxide ion polarizability calculated from the refractive index and the optical band gap.
It is possible to calculate so-called theoretical optical basicity Λth on the basis of the following equation proposed by Duffy and Ingram[4]:
| (1) |
Where, [ X1, X2, ...,Xn ] are the equivalent fractions based on the amount of oxygen, each oxide contributes to the overall glass stoichiometry and Λ1, Λ2, Λn are basicities assigned to the individual oxides.
An alternative approach for the calculation of the optical basicity is the determination of the state of polarization of oxidations in a glass matrix based on the refractive index data.
Duffy[5] has established the following correction:
| (2) |
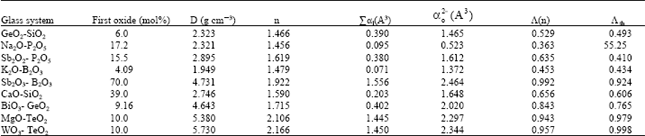
between the optical basicity and the electronic polarizability of the oxide ion for silicates, borates, sulphates and some simple oxides. Duffy has concluded that this relationship presents a general trend toward an increase in oxide ion polarizability with increasing optical basicity (Table 1).
A good agreement can be observed between the optical basicity data with different initial quantities. Most chemical and many physical properties are related to the way in which the electronic charge cloud is distributed over the valence level of atoms or ions constituting a substance. The manner in which the electronic charge is distributed results from synergic effects when one atom interacts chemically with another. Basically, it should be possible to make correlations, at least empirically, between the electronic charge distribution within a material and some of its properties. Correlations of this type, particularly if quantitative, provide a deeper understanding of underlying chemistry or physics and thereby offer the possibility of making useful predictions.
Oxides and many oxidic materials provide a class that is particularly amenable for studying this kind of relationship. Oxygen has an extremely versatile chemistry, forming oxides in which the chemical bonding ranges from highly electrovalent, as in CaO or Na2O, to highly covalent, as in P2O5 (the bonding can also be metallic, e.g., as in TiO and ReO3). As illustrated by these examples, basic oxides are associated with ionicity and acidic ones with covalency, with amphoteric oxides such as Al2O3 being somewhere in-between. This connection between acid/base behavior and the type of chemical bonding dominates many aspects of oxygen chemistry. It is particularly important when dealing with the chemistry and physics of materials that have a covalent network, for example, as in certain phosphates, silicates or borates. These can exist not only as definite compounds, e.g., NaPO3 or CaSiO3, but also as non-stoichiometric glasses.
| Table 1: | Data of optical basicity for some binary system glasses[12] |
 | |
Since glasses are composed of basic (ionic) and acidic (covalent) oxides, it is the final chemical composition that determines its ionic/covalent state. In other words, the extent of negative charge borne by the oxygen atoms is governed by the composition of the glass. The non-stoichiometry of glass thus provides the opportunity for observing the change in a particular property as the oxygen negative charge is gradually increased or decreased (by varying the chemical composition). The extent of negative charge can be expressed using the optical basicity model which was developed in Aberdeen several years ago[1,6].
One of the reasons for conceiving the optical basicity model, in the first place, was to express in numerical terms the acid-base nature of oxidic materials such as glasses and metallurgical slags[6]. Previously, the approach to the acid-base chemistry of melts was based on simplified thermodyamic models featuring oxide ion activities, but these could never be applied rigorously to multicomponent systems[6,7]. Since the inception of optical basicity, its application to problems in extraction metallurgy and the refining power of metallurgical slags, has been met with considerable success[8].
In glass production, exposure to air results in redox interconversion between Fe2+ and Fe3+ ions and these reactions have a profound influence on the quality of the glass product. It appears that the position of equilibrium for most redox reactions correlates very well with the optical basicity value of the glass melt, irrespective of whether the constituent cations are Na+, K+, Ca2+, etc. Before the introduction of the optical basicity model, it was impossible to compare, say, a sodium silicate glass with a potassium silicate glass[6,9]. Correlations of redox chemistry with optical basicity can be used not only for predicting the effect of composition on equilibrium, but also for exploring the chemical bonding interactions that are involved when glasses act as hosts for multivalent cations.
An important application of optical basicity relates to the two site model developed by Kamitsos et al.[10] through studies of cation vibration bands by far-infrared spectroscopy. It now appears that the existence of higher frequency and lower frequency bands correlates with sites of high and low basicity. There remains an open question as to whether or not cations are able to exert chemical preferences to seek out, or generate, sites of high or low basicity. Such choices may influence not only redox properties but also variations in ion mobility and ion exchange properties of glass.
Theoretical considerations: Assuming that molar refractivity (Rm) and polarizability αm are additive quantities Dimitrov and Sakka obtained the relationship[11].
| (3) |
Where, Ri, is ionic refraction of cation, ![]() is the refraction of oxide ion, respectively. P and q denote the number of cation and oxide ion in the chemical formula APOq [13]. This relationship leads to:
is the refraction of oxide ion, respectively. P and q denote the number of cation and oxide ion in the chemical formula APOq [13]. This relationship leads to:
| (4) |
Duffy put an experimental formula for obtaining the polarizability of oxide ion as a function of optical band gap as follows:
| (5) |
Using the Lorenz -Lorenz, equation for simple oxides, Dimitrov and Sakka used the following linear relationship suggested by Duffy and ingram[12]:
| (6) |
Substituting Eq. 6 in Eq. 3, these authors obtained the required relationship between ![]() and Eopt.. This formula was modified to the following relationship;
and Eopt.. This formula was modified to the following relationship;
| (7) |
The values ![]() of for the glass system obtained from the experimentally measured refractive indices and optical bang-gap energies using the Eq. 4 and 5, respectively are used for the optical basicity estimation by using Eq. 2 .
of for the glass system obtained from the experimentally measured refractive indices and optical bang-gap energies using the Eq. 4 and 5, respectively are used for the optical basicity estimation by using Eq. 2 .
| Table 2: | Calculated optical basicity Λ for two ternary glass systems using the refractive index n data and the optical band gap Eopt. |
 | |
| Table 3: | Data of optical basicity with the refractive index (K2O-Nb2O5 -TeO2) |
 | |
| Table 4: | Data of optical basicity with the optical band gap (K2O-Nb2O5 -TeO2) |
 | |
| Table 5: | Data of optical basicity with the refractive index (B2O3 -Na2O -TeO2) |
 | |
| Table 6: | Data of optical basicity with the optical band gap (B2O3 -Na2O -TeO2) |
 | |
The result shows that there is close agreement in the polarizability values obtained from the two different experimental quantities. The agreement is particularly good in view of the possible errors in Eopt due to factors like thickness of the glass samples and the extrapolation method used for evaluating Eopt .
The values of Λ for the glass system obtained from the experimentally measured refractive indices and optical bang-gap energies using the Eq. 4 and 5, respectively are compared (Table 2). The result shows that there is a close agreement in the polarizability values obtained from the two different experimental quantities. The agreement is particularly good in view of the possible errors in Eopt due to factors like thickness of the glass samples and the extrapolation method used for evaluating Eopt .
It is obvious that the two forms (Eq. 4 and 5) can be used to estimate the optical basicity of the glass system and the more accurate refractive index and optical band gap data are, the less the error δΛ of the optical basicity is where:
| (8) |
As referred in earlier paragraph,the optical basicity of numerous simple oxides has been determined by Dimitrov and Sakka[3]using Eq. 2 on the basis of the average electronic polarizability of oxide ions calculated from the refractive index α02¯ (n) and energy gap α02 (Eopt.).
In the present study we investigate whether the optical basicity approach used for binary oxide glasses or simple oxides can be extended to ternary system glasses.
The optical basicity for two ternary oxide glasses presented in Table 2 using
Eq. 2. The obtained values of Λ are represented versus the n values of the first system (Table 3), also the calculated values of Λ depending on Eopt., are ploted in (Table 4) against Eopt.
Table 5 and 6 show the same relations for the second glass system.
The importance of these tables is represented in the uncertainty of Λ as there is an error in the determination of n and Eopt., especially Eopt. as it is obtained by extrapolation and fitting.
The K2O-Nb2O5-TeO2 glass system has Λth ~0.8 and Λ(n) ~ 0.835 i.e the uncertainty δΛ = ± 7% on the other hand the uncertainty δΛ(Eopt.) = ± 15% . Also B2O3-Na2O-TeO2 has Λth = 0.571 and Λ(n) = 0.9 and Λ(Eopt.) = 0.68, generally we can say that as the refractive index and optical band gap are more accurate, as the accurate estimation of the optical basicity of the glass system. Fortunately, it is obvious that the relation between Λ(n) and n or Λ(Eopt.) and Eopt are nearly linear, so we can estimate (δΛ/δn) and (δΛ/δEopt.) simply in the range of small refractive index change (error of n or error of optical band gap).
CONCLUSIONS
The optical basicity Λ has been evaluated depends on the optical band gap and the refractive index data for two different ternary glass systems. Also the uncertainty of Λ in the two cases was estimated, hence we can predict the accurate method for the optical basicity calculations. It has been established that there is a general trend of increasing the oxide ion polarizability with decreasing the oxide optical band gap and increasing the refractive index n. Also I would like to say that the present study is a smoothly investigation for the concept of the optical basicity in case of ternary glass oxide systems.








