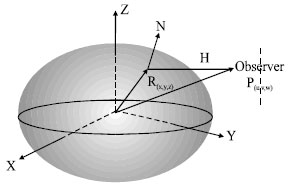
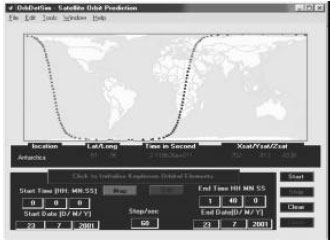
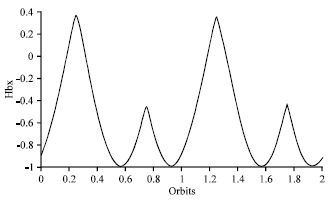
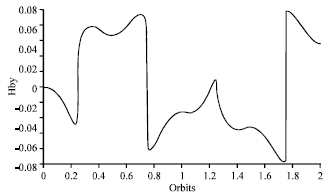
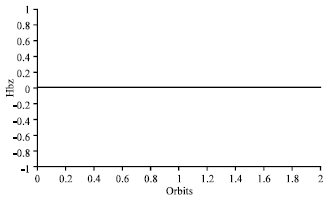
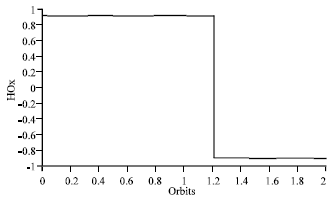
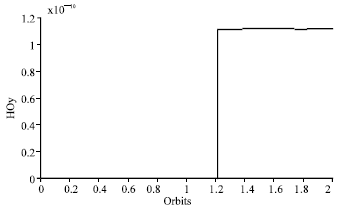
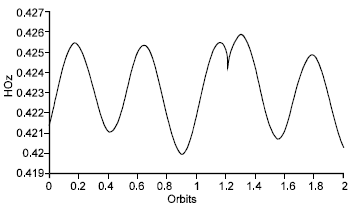
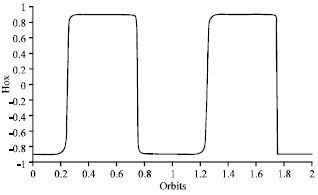
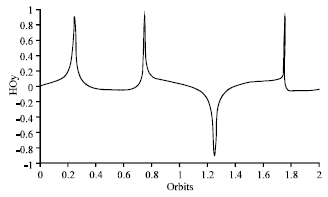
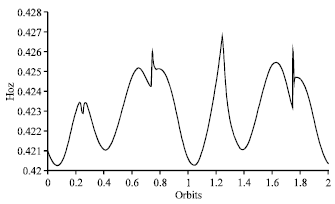
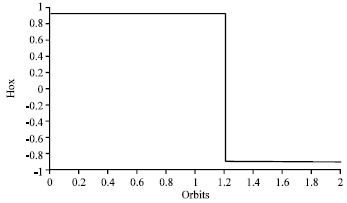
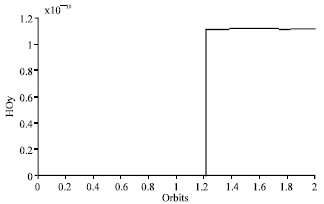
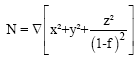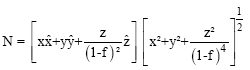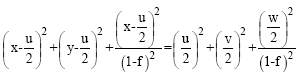Research Article
Sensor Vectors Modeling for Small Satellite Attitude Determination
Department of Data Processing, Industrial Optimization and Modelisation Laboratory, University of Sciences and Technology of Oran, USTO, BPI 505, EL M Noouar, Oran, Algeria
M. Benyettou
Department of Data Processing, Industrial Optimization and Modelisation Laboratory, University of Sciences and Technology of Oran, USTO, BPI 505, EL M Noouar, Oran, Algeria
A. Si Mohammed
Department of Data Processing, Industrial Optimization and Modelisation Laboratory, University of Sciences and Technology of Oran, USTO, BPI 505, EL M Noouar, Oran, Algeria