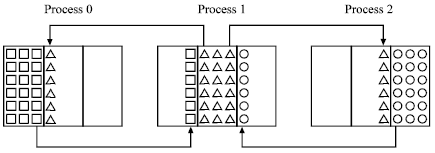
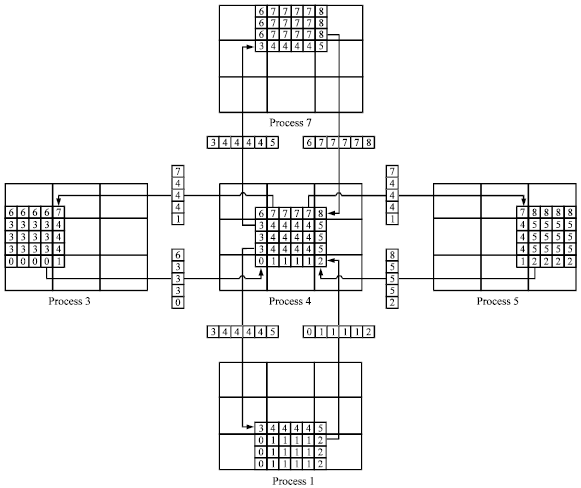
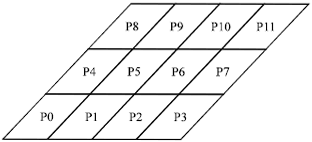
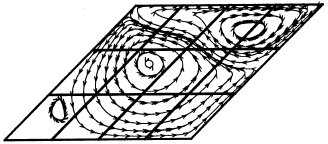
Research Article
Large Eddy Simulations of Turbulent Flow Across Tube Bundle Using Parallel Coupled Multiblock Navier-Stokes Solver
Department of Mechanical Engineering, Isf�han University of Technology, Isfahan, Iran
E. Shirani
Department of Mechanical Engineering, Isf�han University of Technology, Isfahan, Iran
M. Ashrafizaadeh
Department of Mechanical Engineering, Isf�han University of Technology, Isfahan, Iran