Research Article
Wheather Optimal Seignorage Exists in SARC Countries
Department of Economics, University of Hacettepe, Beytepe Campus, Ankara, Turkey
Ahmet Sahinoz
Department of Economics, University of Hacettepe, Beytepe Campus, Ankara, Turkey
Throughout most of recent history, inflation rates, tax rates and creation of money rates move in same direction with same magnitude. They show very little reversion to any normal level. Kirschen[1] report the findings of non-stationary in the rate of inflation over the post-war period. Inflation is one form of taxation. It is a tax on holding money balances. Beyond the traditional deadweight losses of tax, inflation also imposes many other social cost[2]. If the marginal social cost of raising revenue is increasing in the tax rate, as one would typically expect, optimal fiscal policy entails the smoothing of tax rate over time[3]. The general principle to the case of seigniorage implies that nominal interest rate and inflation should be smoothed as well and that such smoothing make these series approximately random walks.
Friedman[4] and Bailey[5] have considered the question of the optimal level of revenue from money creation in steady state. More over, drawing on the tax smoothing literature[6] it has been argued that an optimising government would set the rate of tax derived from currency issue in such a manner as to equalize the marginal deadweight loss from this and other sources of tax revenue[7]. However, the empirical relevance of this proposition is questionable, especially if it is taken to imply that revenue from inflation and other taxes will be correlated over time[8,9]. Especially in developing and transition economies, resort to the inflation tax is often an unplanned response to a fiscal crisis, often surging when other tax revenue falls off.
Jefferson[10] extends the study of Barro[3] to a longer time period, which allows him to check whether the importance of seigniorage in government financing continued to persist throughout later periods. Furthermore, he takes up the idea that a considerable part of US seigniorage comes from the rest of the world, especially from emerging and transitional economies unable to provide their residents with stable national monies[10].
His calculations for the overlapping period with the Barro[3] study, 1977 to 1981, show slightly diverging numbers. The ratios of seigniorage revenue to tax receipts and GNP show the peak of this revenue source in the early and mid 1980s for the net Federal revenues and the opportunity cost measure of seigniorage (inflation tax).
Money creation, as every distortionary form of taxation, is inferior to lump-sum taxation as a revenue device for the government. However, the ease of collecting this specific kind of a tax, the low cost of printing money and the fact that the burden of seignorage falls on those holding the currency, which might to a great extent be nonresidents, speaks in favor of it. In the US from 1948-89 seigniorage accounted for less than two percent of total federal government revenues and for approximately 0.3% of GNP[2]. Obstfeld and Rogoff[11] display very similar numbers for the importance of seignorage for the United States for a more recent time period. According to them, from 1990 to 1994 seignorage revenues helped to finance 2.19% of the US government spending and amounted to 0.44 % of GDP.
The size of the quasi-tax represented by reserve requirements along with interest ceilings and explicit taxes on bank interest receipts, is quantitatively very important in many countries[12].
Given the time path of government expenditure, how should government finance its expenditure? In this connection, Mankiw[7] develop a simple model to analyze the optimal financial policy of the government in a monetary economy. He derives the optimal rule, which implies that the rate of income tax and the rate of inflation follow random walk processes and these two rates have positive correlations. He regress the tax rate on the rate of inflation and finds a positive significant coefficient for the United State, while Poterba and Rotemberg[13] find that the cases of United States and Japan are consistent with the optimal seigniorage model. Mankiw[7], Poterba and Rotemberg[13] used the OLS method to obtain optimal rule between the rate of income tax and the rate of inflation. There findings are reexamineded by Fukuta and Shibata[14] with tools of unit root test and found no validity of optimal seignorage model for those countries.
The model presented here to formalize above ideas into empirically version. The model can be interpreted in two ways. In one way, we look the relationship between inflation rate and tax rate, on other hand we analyse the relationship between creation of money rate and inflation rate in South Asian Regional Co-operation countries.
| (1) |
Where, G, T and B represent government expenditure, the total revenues of the government, total value of government bonds and ρ denotes discounte rate, it is assumed as constant.
For the moment, the demand for money is described as:
| (2) |
Where, M, P and Y stand for nominal money balances, the general price level and national income, respectively. From this the value of seigniorage is given by as:
| (3) |
Where, g = ΔY/Y and π = ΔP/P represent the growth rate of GNP and inflation rate, respectively.
Here, we assume that the rate of taxation on income is τ, then we derive the government’s total revenues taxation and new printed money as follow:
| (4) |
The deadweight social losses induced by money creation, H, are described as: H = [h (II) y], where, h’>0 and h">0 The deadweight social losses are assumed homogeneous in output.
Similarly, the deadweight social losses induced by the tax are denoted as F = f(τ)Y, where, f" 1>0 and f"’2>0.
Total revenues can be given such as:
The main objective of the government is to minimize the value of social losses
| (5) |
Subject to budget constraint:
| (6) |
As in much empirical work has studied by Hall[15], Hansen and Sinleton[16], Mankiw[7] therefor, we do not solve for decision rule but rather examine the first-order conditions necessary for an optimum. The first order conditions are
| (7) |
| (8) |
These equations given the optimal policy of the government. The intertemporal first-order condition (7) equates the marginal social cost of taxation today and in future. The intertemporal first-order condition (8) equates the marginal social cost of raising revenue through direct taxation and the marginal social cost of raising revenue through seignorage.
Data and sample characteristics: Annual data on tax rates, inflation rate and creation of money rates of SARC countries for the 1950-2003 period were taken from the IMF International Financial Statistics. Using annual data, firstly, we check the series whether or not contain unit root. The sample countries are Bangladesh, Bhutan, India, Maldives, Nepal, Pakistan and Sri Lanka. We take central government tax revenues per GNP as of the tax rate and money per GNP as of the rate of money creation. The rates of inflation are calculated from the Consumer Price Index.
Table 1 shows the results of unit roots tests for each variable. To examine the stationary of respective time series, we develop we-llknown Dickey-Fuller, Augmented Dickey-Fuller[17] unit root test and Phillips and Perron’s[18] test.
| Table 1: | Unit root test for the inflation rates, tax rates and money supply |
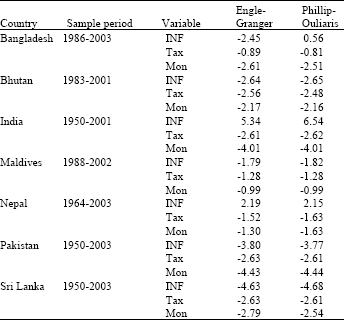 | |
Critical values for the ADF statistics from Fuller[17] Table 8.5.2. p:373.1976. Critical values of DF Statistics are -3.58, -2.93 and -2.60 at 1, 5 and 10% levels | |
We find in Table 1 that tax rate, inflation rate and rate of money creation have unit roots in Bangladesh, Bhutan, Maldives and Nepal while these series have no unit roots in the series data of India, Pakistan and Sri Lanka.
Table 2 reports the results of cointegration tests by Engle and Granger’s[19], Dickey-Fuller[17] tests and Phillips and Ouliaris[18]. Results show that there are cointegration relationship between the tax rate and inflation rate in case of India and the creation of money rate and inflation rate in case of Buhtan, Notwithstanding, there are no cointegration relationship between the tax rate, inflation rate in case of Bangladesh, Bhutan, Maldives, Nepal, Pakistan and Sri Lanka.
| Table 2: | Cointegration tests for the inflation rates and tax rates |
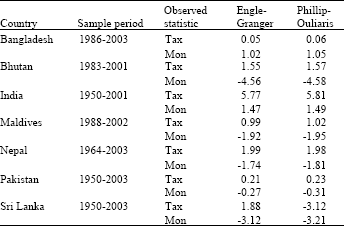 | |
Critical values of the DF statistics are -3.03, -3.37 and -4.07 at the 10, 5 and 1% levels. Critical values of the ADF statistics are -2.77, -3.17 and -3.77 at the 10, 5 and 1% levels. Sources: Engle and Granger[19], Philips and Ouliaris[18] | |
Similarly, there are no cointegration relationship between the creation of money rate and inflation rate in case of Bangladesh, India, Maldives, Nepal, Pakistan and Sri Lanka
In nutshell, we conclude that optimal seignorage model exist in India in version of tax rate and in Bhutan in version rate of creation of money rate.
In this study we have tested the optimal seigniorage model developed by Mankiw[7] for Bangladesh, Bhutan, India, Maldives, Nepal, Pakistan and Sri Lanka. Empirical evidence presented in this article suggests that cointegration relationship exist between the tax rate and inflation rate in case of India and the creation of money rate and inflation rate in case of Buhtan. Moreover, the model is rejected in respect of all other countries.