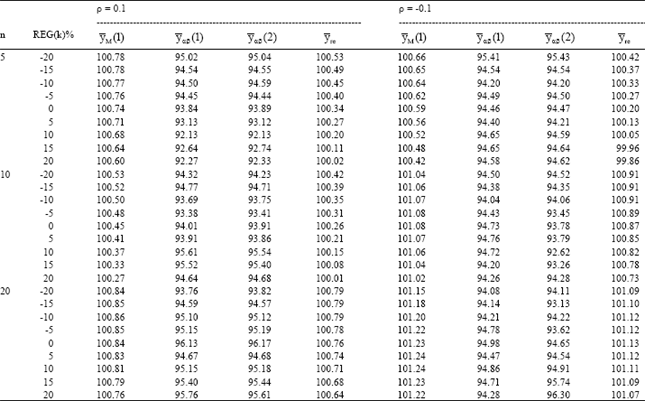
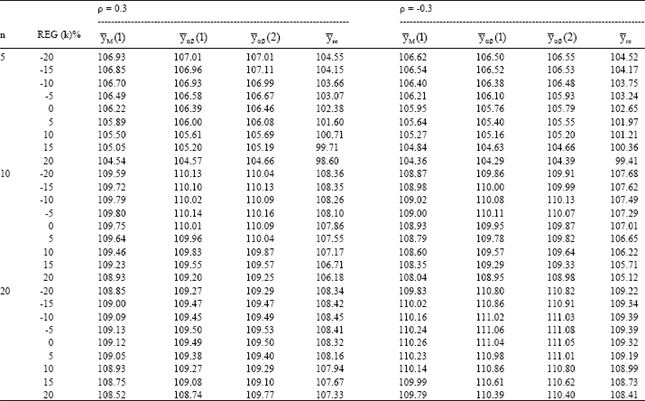
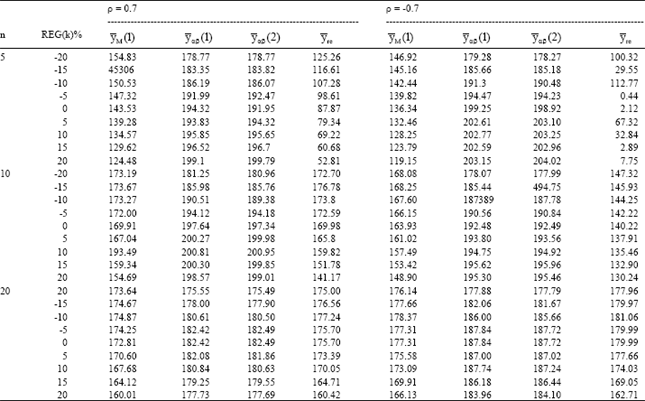
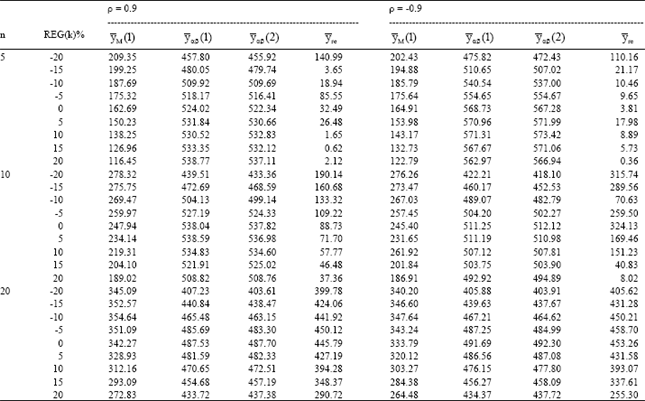
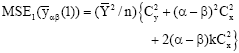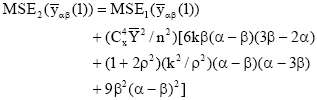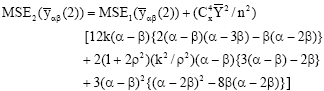Research Article
Using Meta-analysis for Data Enrichment-optimal Families of Estimation Strategies
Department of Statistics and Demography, University of Swaziland, Kwaluseni, P. Bag 4, Swaziland, Africa
M. Mahibbur Rahman
Department of Statistics and Demography, University of Swaziland, Kwaluseni, P. Bag 4, Swaziland, Africa
Rameshwar P. Jaju
Department of Computer Science, University of Swaziland, Kwaluseni, P. Bag 4, Swaziland, Africa