Research Article
An EOQ Model Under Trade Credit Linked to Order Quantity Using Algebraic Method
Department of Business Administration, Chaoyang University of Technology, Taichung, Taiwan, Republic of China
Several studies have carried out previously treat inventory problems with varying conditions under the consideration of permissible delay in payments.
Goyal[1] established a single-item inventory model under permissible delay in payments. Chung[2] developed an alternative approach to determine the economic order quantity under condition of permissible delay in payments. Aggarwal and Jaggi[3] considered the inventory model with an exponential deterioration rate under the condition of permissible delay in payments. Chang et al.[4] extended this issue to varying rates of deterioration. Liao et al.[5] and Sarker et al.[6] investigated this topic in the presence of inflation. Jamal et al.[7] and Chang and Dye[8] extended this issue with allowable shortage. Chang et al.[9] extended this issue with linear trend demand. Chen and Chuang[10] investigated a light buyer’s inventory policy under trade credit by the concept of discounted cash flows. Hwang and Shinn[11] modeled an inventory system for retailer’s pricing and lot sizing policy for exponentially deteriorating products under the condition of permissible delay in payment. Jamal et al.[12] and Sarker et al.[13] addressed the optimal payment time under permissible delay in payment with deterioration. Teng[14] assumed that the selling price was not equal to the purchasing price to modify Goyal’s model[1]. Chung et al.[15] discussed this issue under the assumptions that the selling price is not equal to the purchasing price and different payment rules. Khouja and Mehrez[16] investigated the effect of four different supplier credit policies on the optimal order quantity within the EOQ framework. Shinn and Hwang[17] determined the retailer’s optimal price and order size simultaneously under the condition of order-size-dependent delay in payments. They assumed that the length of the credit period is a function of the retailer’s order size and also the demand rate is a function of the selling price. Chung and Huang[18] examined this problem within the EPQ framework and developed an efficient procedure to determine the retailer’s optimal ordering policy. Huang[19] extended this issue under two levels of trade credit and developed an efficient solution procedure to determine the optimal lot-sizing policy of the retailer. Huang and Chung[20] extended Goyal’s model[1] to cash discount policy for early payment.
Goyal[1] is well known when the inventory systems under conditions of permissible delay in payments and implicitly makes the following assumption. Supplier credit policy offered to the retailer where credit terms are independent of the order quantity. That is, whatever the order quantity is small or large, the retailer can take the benefits of payment delay. Under this condition, the effect of stimulating the retailer’s demand may be reduced. So, the present study will adopt the following assumption to modify the Goyal’s model[1]. To encourage retailer to order a large quantity, the supplier may give the trade credit period only for a large order quantity. In other words, the retailer requires immediate payment for a small order quantity. This viewpoint can be found in Khouja and Mehrez[16] and Chang et al.[21].
In addition, in previous study which have been derived using differential calculus to find the optimal solution and the need to prove optimality condition with second-order derivatives. The mathematical methodology is difficult to many younger students who lack the knowledge of calculus. In recent study, Grubbström and Erdem[22] and Cárdenas-Barrón[23] showed that the formulae for the economic order quantity (EOQ) and economic production quality (EPQ) with backlogging could be derived without differential calculus. They mentioned that this approach must be considered as a pedagogical advantage for explaining the EOQ and EPQ concepts to students that lack knowledge of derivatives, simultaneous equations and the procedure to construct and examine the Hessian matrix. Therefore, we want to adopt the algebraic method to investigate the effect of trade credit policy depending on the order quantity within the economic order quantity (EOQ) framework. Then, two theorems are developed to efficiently determine the optimal cycle time and optimal order quantity for the retailer. Finally, numerical examples are given to illustrate these theorems obtained in the present study.
| Algebraic model formulation | ||
| Notation | ||
| Q | = | Order quantity |
| D | = | Annual demand |
| W | = | Minimum order quantity at which the trade credit is permitted |
| A | = | Cost of placing one order |
| c | = | Unit purchasing price per item |
| h | = | Unit stock holding cost per item per year excluding interest charges |
| Ip | = | Interest charges per $ investment in inventory per year |
| Ie | = | Interest which can be earned per $ per year |
| M | = | The trade credit period |
| T | = | The cycle time |
| TRC(T) | = | The annual total relevant cost when T>0 |
| T* | = | The optimal cycle time of TRC(T) |
| Q* | = | The optimal order quantity=DT* |
| Assumptions | |
| 1. | Demand rate is known and constant |
| 2. | Shortages are not allowed |
| 3. | Time period is infinite |
| 4. | Replenishments are instantaneous with a known and constant lead time |
| 5. | If Q<W, i.e. T<W/D, the trade credit is not permitted. Otherwise, fixed trade credit period M is permitted. Hence, if Q<W, pay cQ when the order is received. If Q≥W, pay cQ M time periods after the order is received |
| 6. | During the time the account is not settled, generated sales revenue is deposited in an interest-bearing account. When T≥M, the account is settled at T=M, the retailer starts paying for the higher interest charges on the items in stock. When T≤M, the account is settled at T=M and the buyer does not need to pay any interest charge |
| 7. | Ip ≥ Ie |
The annual total relevant cost consists of the following elements. Two situations arise. (I) M≥W/D and (II) M<W/D
| Case I: Suppose that M≥W/D | |
| 1. | Annual ordering cost = A/T |
| 2. | Annual stock holding cost (excluding interest charges) = DTh/2 |
| 3. | There are three cases in terms of cost of interest charges for the items kept in stock per year. (I) : 0<T<W/D In this case, the retailer must pay cDT when the order is received since the trade credit is not permitted. Therefore, Cost of interest charges for the items kept in stock per cycle = cIpDT2/2 Cost of interest charges for the items kept in stock per year = cIpDT/2 (ii) : W/D≤T≤M In this case, the fixed trade credit period M is permitted since Q≥W. According to assumption (6), no interest charges are paid for the items kept in stock (iii) : M≤T In this case, the fixed trade credit period M is permitted since Q≥W. According to assumption (6), Cost of interest charges for the items kept in stock per cycle = cIpD(T-M)2/2 Cost of interest charges for the items kept in stock per year = cIpD(T-M)2/2T |
| 4. | There are three cases in terms of interests earned per year. (I) : 0<T<W/D In this case, no interest earned since the trade credit is not permitted. (ii) : W/D≤T≤M In this case, the fixed trade credit period M is permitted since Q≥W. According to assumption (6), Interests earned per cycle |
| (iii) : M≤T In this case, the fixed trade credit period M is permitted since Q≥W. According to assumption (6), | |
From the above arguments, the annual total relevant cost for the retailer can be expressed as:
TRC(T) = ordering cost + stock-holding cost + interest payable-interest earned. It is shown that the annual total relevant cost, TRC(T), is given by
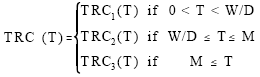 | (1a) (1b) (1c) |
where
| (2) |
| (3) |
and
| (4) |
Since TRC1(W/D)>TRC2(W/D), TRC2(M)=TRC3(M), TRC(T) is continuous except T=W/D.
Then, we can rewrite
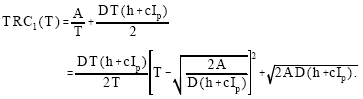 | (5) |
Equation (5) represents that the minimum of TRC1(T) is obtained when the quadratic non-negative term, depending on T, is made equal to zero. Therefore, the optimum value T1* is
| (6) |
Therefore, equation (5) has a minimum value for the optimal value of T1* reducing TRC1(T) to
| (7) |
Similarly, we can derive TRC2(T) without derivatives as follows:
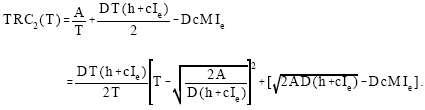 | (8) |
Equation (8) represents that the minimum of TRC2(T) is obtained when the quadratic non-negative term, depending on T, is made equal to zero. Therefore, the optimum value T2* is
| (9) |
Therefore, equation (8) has a minimum value for the optimal value of T2* reducing TRC2(T) to
| (10) |
Likewise, we can derive TRC3(T) algebraically as follows:
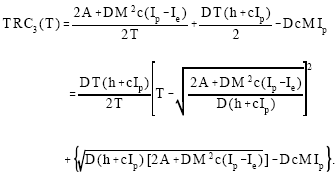 | (11) |
Equation (11) represents that the minimum of TRC3(T) is obtained when the quadratic non-negative term, depending on T, is made equal to zero. Therefore, the optimum value T3* is
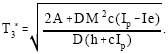 | (12) |
Therefore, equation (11) has a minimum value for the optimal value of T3* reducing TRC3(T) to
| (13) |
Case II: Suppose that M<W/D: If M<W/D, equations 1(a, b, c) will be modified as
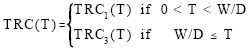 |
Since TRC1(W/D)>TRC3(W/D), TRC(T) is continuous except T=W/D.
Determination of the optimal cycle time T*
(1) When M≥W/D: Above equation (6) implies that the optimal value of T for the case of 0<T<W/D, that is 0<T1*<W/D. We substitute equation (6) into 0<T1*<W/D, then we can obtain the optimal value of T
| (14) |
Similarly, equation (9) implies that the optimal value of T for the case of W/D≤T≤M, that is W/D≤T2*≤M. We substitute equation (9) into W/D≤T2*≤M, then we can obtain the optimal value of T
| (15) |
Finally, equation (12) implies that the optimal value of T for the case of T≥M, that is T3*≥M. We substitute equation (12) into T3*≥M, then we can obtain the optimal value of T
| (16) |
Furthermore, we let
| (17) |
| (18) |
and
| (19) |
From equations (17), (18) and (19), we can easily obtain Δ3 ≥ Δ2. In addition, we know TRC1(W/D)>TRC2(W/D), TRC2(M)=TRC3(M), TRC(T) is continuous except T=W/D from equations (2), (3) and (4). Then, we can summarize above arguments and obtain following results:
| Theorem 1 | |
| 1. | If Δ1>0, Δ2>0 and Δ3>0, then TRC(T*)=min {TRC1(T1*), TRC2(W/D)}. Hence T* is T1* or W/D associated with the least cost. |
| 2. | If Δ1>0, Δ2≤0 and Δ3>0, then TRC(T*)=min {TRC1(T1*), TRC2(T2*)}. Hence T* is T1* or T2* associated with the least cost. |
| 3. | If Δ1>0, Δ2≤0 and Δ3≤0, then TRC(T*)=min {TRC1(T1*), TRC3 (T3*)}. Hence T* is T1* or T3* associated with the least cost. |
| 4. | If Δ1≤0, Δ2>0 and Δ3>0, then TRC(T*)=TRC2(W/D) and T*=W/D. |
| 5. | If Δ1≤0, Δ2≤0 and Δ3>0, then TRC(T*)=TRC2 (T2*) and T*=T2*. |
| 6. | If Δ1≤0, Δ2≤0 and Δ3≤0, then TRC(T*)=TRC3(T3*) and T*=T3*. |
(2) When M<W/D: In another condition M<W/D, equations 1(a, b, c) will be modified as
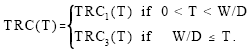 |
Similarly, equation (6) implies that the optimal value of T for the case of 0<T<W/D, that is 0<T1*<W/D. We substitute equation (6) into 0<T1*<W/D, then we can obtain the optimal value of T
| (20) |
Likewise, equation (12) implies that the optimal value of T for the case of T≥W/D, that is T3*≥W/D. We substitute equation (12) into T3*≥W/D, then we can obtain the optimal value of T
| (21) |
Furthermore, we let
| (22) |
and
| (23) |
We know TRC1(W/D)>TRC3(W/D), TRC(T) is continuous except T=W/D from equations (2) and (4). Then, we can summarize above arguments and obtain following results:
| Theorem 2 | |
| 1. | If Δ1 > 0 and Δ4 > 0, then TRC(T*)=min {TRC1(T1*),TRC3(W/D)}. Hence T* is T1* or W/D associated with the least cost. |
| 2. | If Δ1 ≤ 0 and Δ4 ≤ 0, then TRC(T*)=TRC3(T3*) and T*=T3*. |
| 3. | If Δ1 > 0 and Δ4 ≤ 0, then TRC(T*)=min {TRC1(T1*),TRC3(T3*)}. Hence T* is T1* or T3* associated with the least cost. |
| 4. | If Δ1 ≤ 0 and Δ4 > 0, then TRC(T*)=TRC3(W/D) and T*=W/D. |
Numerical examples: To illustrate all results obtained in the present study, let us apply the proposed method to efficiently solve the following numerical examples.
| Table 1: | The optimal cycle time and optimal order quantity with various values of W and c |
 | |
To study the effects of the minimum order quantity to obtain the permissible delay, W and unit purchasing price per item, c, on the optimal cycle time and optimal order quantity for the retailer derived by the proposed method, we solve the example in Table 1 with various values of W and c. The following inferences can be made based on Table 1. When W is increasing, the optimal cycle time and optimal order quantity for the retailer will not decrease. It implies that the retailer will order more quantity to take the benefits of trade credit as much as possible when the minimum order quantity to obtain the trade credit is higher. When c is increasing, the optimal cycle time and optimal order quantity for the retailer are not increasing. This result implies that the retailer will not order more quantity to take the benefits of the trade credit more frequently.
The supplier offers the trade credit policy to stimulate the demand of the retailer in general. For reaching the effect of trade credit, the supplier may give the trade credit period only for a large order quantity. In other words, the retailer requires immediate payment for a small order quantity. This situation is very reasonable in the real business transactions. We develop the retailer’s inventory model in this situation. These results are very helpful to the inventory replenishment decision-makers.
Future study may further incorporate the proposed model into more realistic assumptions, such as allowable shortages, limited storage capacity and a finite rate of replenishment.
The author would like to thank that this study is partly supported by NSC Taiwan, project No. NSC 92-2213-E-324-014.