Research Article
The Role of Centrifugal Pumps in Water Supply
Faculty of Engineering, Al-Isra University, P.O. Box 99, 11622 Amman, Jordan
Bassam A. Al- Helou
Faculty of Engineering, Al-Isra University, P.O. Box 99, 11622 Amman, Jordan
Pumping is a vital method for supply water from some resources, which the gravity system cannot be enough due the effect topography and side levels[1]. This method may also locate at surface sources including rivers, canals, lakes, as well as groundwater basins and wells.
Pumps are considered part of turbo machines, which convert mechanical energy into water energy, or it absorb power to raise pressure head to transfer water from low level to high level. These machines are classified as centrifugal, reciprocating, pneumatic, jet and rotor types based on the purpose and type of fluid used. The centrifugal pumps involving, radial, axial or mixed are the common types of pumps used for water transfer, due to presence of impeller and centrifugal action. Fluid enters the impeller in the center portion, called eye and discharges around the entire circumference in a casing. During rotating, the liquid receives energy from the vanes and resulting in an increase of pressure and absolute velocity. The larger part of the energy is kinetic and then it is transformed into pressure head. This is accomplished in the volute casing surrounding the impeller. The demand for greater capacity without increasing the diameter resulted in an increase in the dimensions parallel to the shaft. This requires an increase in the eye diameter to accommodate the larger flow and corresponding change in the vanes at entrance. A further increase in specific speed is obtained with the propeller or axial flow pump[2].
Also, centrifugal pumps are divided into two general classes; volute and diffuser pumps. In the former, the impeller is surrounded by a spiral case and the outer boundary called a volute. In the diffuser, the impeller is surrounded by vanes provided gradually enlarging passage to affect a gradual reduction in velocity. Besides that, centrifugal pumps are mounted as single and double suction pumps. The latter have the advantage of symmetry to eliminate end thrust. A pump is rated by its capacity and heads at the point of the maximum efficiency for a given rotate speed. These values refer as normal capacity for that speed[3].
The scope of the present study is to express the role of centrifugal pump in water systems as a tool of lifting pipe flow from one level to another. This study has been done through theoretical analysis as well as experimental investigation.
Centrifugal pumps normally apply momentum equation for determining the force on a curved bladed. The absolute velocity of the water is resolved into sub-components in the radial, tangential and axial directions. The force in any direction is derived from the change of the momentum in that direction. The tangential velocity component to the rotor circumference is called the velocity of the whirl and considers the most important part of the velocity which gives rise to the torque and power. With respect to Euler equation, the power input[3]:
| (1) |
| Where: | ||
| ρ | = | Density kg/m3, |
| Q | = | Discharge m3/s, |
| U2 | = | Outlet velocity m s-1, |
| r2 | = | Radius outlet m, |
| U1 | = | Inlet velocity m s-1, |
| r1 | = | Radius inlet m, |
| ω | = | Angle velocity 1 s-1. |
For pump analysis, it is convenient to use head product rather than the power input. But, the head H represents the energy per unit weight. Then
| (2) |
by inserting Equation 1 into Equation 2 :
| (3) |
but, ω.r1 = V1 , ω.r2 = V2
where:| V1 | = | Tangential velocity of blade at inlet, |
| V2 | = | Tangential velocity of blade at outlet. |
then,
| (4) |
The general arrangement of a centrifugal pump shows that the water enters the casing in an axial direction, but it is turned through 90° before entering the impeller, then passes after that through the blades to enter the volute chamber. At inlet to the impeller, the water velocity has no component in the tangential direction (U1=0.0) and the velocity triangle is right angled. Hence:
| (5) |
Based on that, the Euler head is greater than the actual head produced due to the losses. But the actual head comprises the suction head (Hs), the discharge head (Hd), the friction losses in the suction (Hfs), the friction losses in discharge (Hfd) and the discharge velocity head (Vd2/2g). This head is known as manometric head (Hm). In other words,
| (6) |
from that, the ratio of the manometric head to the Euler head is called the manometric efficiency, ηm, or
| (7) |
If the velocity head is neglected and the impeller losses are considered the efficiency of the pump is affected. Then the total head must be developed to overcome the impeller and the system losses in the pipe lines and pipe lifting. But efficiency of pumping suction depends much on the piping system used to convey the fluid.
In other words, losses are overcomes by the pump characteristic, which is a function of discharge and is expressed mathematically as[4]:
| (8) |
Also, the performance of the pump is interrelated which external pipe, which is given by[5]:
| (9) |
where:
A, B and C are constants depend on discharge used to specify a pump curve, Hs=static head or suction head and K=constant depends on discharge and the external pipes.
The analytical of the equation 8 and 9 gives the duty point at which the pump delivers the required discord coinciding with the peak efficiency and economical manner. Figure 1 represented the pump characteristics as well as the pipe lines system.
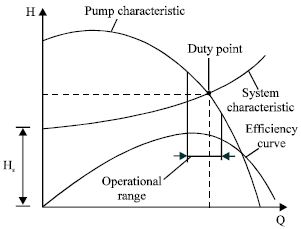 | |
| Fig. 1: | Pump and pipeline characteristics[6] |
Besides that, the pump may be operated under various speeds in order to reply with the need and characteristics variation according to that. There fore, the corresponding discharge, head and power can be giving as following[7]:
| (10) |
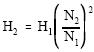 | (11) |
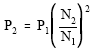 | (12) |
In addition to that, several pumps can be operated in series or in parallel in order to increase the head and discharge, respectively. These pumps can be located individually or in multistage. But to avoid cavitation for these pumps, the suction head omitted so that the pressure at the inlet is equal to the allowable vapor pressure, where the critical cavitation number is suggested as:
| (13) |
Where: Ns specific speed of the pump.
Experiments were conducted in centrifugal a pump (FM 20 demonstration unit) connected to computer IBM.
Notation and dimensions are shown on the diagram (Fig. 2). A reservoir and pipework for continuous water circulation are included. Manually operated valves at the pump inlet and outlet allow control of the flow and also facilitate study of suction effects. Flow rate is monitored by an orifice plate. The pump is single-stage and is driven by a close coupled 180 W ac induction motor.
In normal, a menu-driven software allows the operator to capture data samples from the equipment and facilities automatic calculation of relevant parameters to demonstrate the performance and behavior of the equipment. The performance is related to the flow rate, which is adjusting by using valve situated in the pump discharge pipe. Samples are taken in sequence between minimum and maximum flow rate and then they are monitored by measurement of differential pressure across an orifice plate. The results will demonstrate the equipment speed characteristics, but motor speed should be reset after each adjustment. Also, the variables in the program are based on the equations recommended in BS 5316 (Acceptance test for centrifugal pump). Simplified versions of the equations have been used to reduce the complexity of the calculations.
Before taking data, two conditions of the valve (from the tank to the pump inlet) were configured. The former (constant voltage) showed that the valve was initial closed then it was opening gradually. The later (valve opened) represented the variable of the voltage progressively. By using the obtained data, the relation between the volumetric discharge and number of parameters. Including head, power and efficiency were shown graphically.
The relation between the volumetric flow rate and the head within two previous conditions is shown in Fig. 3.
 | |
| Fig. 2: | Apparatus diagram 1-reservoir, 2-discharge control valve, 3-orifice plate, 4-pressure head sensor across the orifice plate, 5-temperature sensor, 6-pressure head sensor across the pump, 7-pump, 8-capture, 9-transformer, 10-PC |
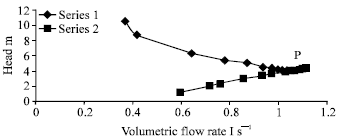 | |
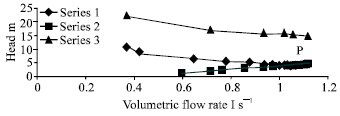
| Fig. 3: | Relation between head and volumetric flow rate |
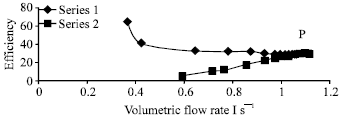 | |
| Fig. 4: | Relation between efficiency and volumetric flow rate |
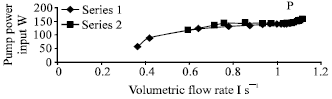 | |
| Fig. 5: | Relation between pump power input and volumetric flow rate |
 | |
| Fig. 6: | Theoretical and experimental results of head against discharge |
It was seen that the head decreases with increasing discharge at constant voltage till the point P. While at variable voltage the head increases with increasing discharge till that point. Beyond that, the head became constant.
The relation between the efficiency and the volumetric flow rate is presented in Fig. 4. Series 1, shows efficiency decreasing with discharge increasing, while series 2 expresses direct proportional of increase for discharge for both. Downward of point P, they followed the same horizontal line.
The relation between the input power and the mass flow rate is shown in Fig. 5. For both conditions, the input power increased progressively with mass flow rate until point. P. Beyond that it was look like constant.
It was shown that the point (P) represents the duty point which shows that the pump delivers required discharge at that position coincide with the peak efficiency of economical operating. For varying discharge it may be throttled over an operating range, but still have to be limited to one giving reasonably high pump efficiency. For various pipe lines, it must be noted that each operational point corresponded to a particular efficiency and the selection of pipe lines largely depends on discharge and pump efficiency.
With references to the previous equations and figures it is shown that the pumps convert mechanical energy into water energy. Also, the efficiency largely depends on the piping system, because the best diameter of pipe line relays on the system characteristics as well as pump characteristics. Besides that, it is convenient to use head product rather than the power input in order to analyse the pump work. Based on that, the theoretical analysis and the experimental results of the relation of head and discharge are shown in Fig. 6.
From that, it is seen that series (1) matches the theoretical line towards point (P), while series (2) moves in different path. Downward, both cases of experimental results and theoretical follow approximately horizontal line. This means, that the important position in the diagram is point (P), which represents the duty point, or it is a sign of economical operation with high efficiency. Beyond that, the pump can be worked with less efficiency without modification, or it will create a lot of problems including caviation or other defects. In order to avoid these conditions it is necessary to concentrate much how to find out the duty point during the work of model in the labor the prototype in the field.
In addition to that it is useful to study the variation of head, discharge and power according to the increase or decrease of specific speed.
Centrifugal pumps are the suitable tools for lifting water, due to its small size, high speed, high pressure and cheap price.
A number of parameters are considered through the analysis of pump work, including capacity, speed and efficiency. But the produced head is the attractive measurement of the transformation of the mechanical energy into kinetic and potential energy. Results, showed that there is a point on the obtained curve represents the maximum efficiency with economic operation known as duty point. Therefore, the acceptable design conditions may happen either in excess or below the capacity at the best efficiency.
In addition to that, the minimum required for a given speed is to avoid cavitation through identified the difference between the absolute suction head and the vapor pressure at pumping temperature.
Finally, pumps that operate at reduced capacity do not have long life as pumps operated at close to their best efficiency. Otherwise, more than one pump is necessary for the system.
Mia Evans Reply
Thanks for helping me understand that the piping system will also affect the efficiency of the processes, because of the diameter of pipelines and the pump characteristics. I will make sure that I will look at my options and ask professionals what they can recommend for the type of property I have. It's important for me that we have a proper water well pump installation with the right materials.
Editor
You're very welcome! I'm glad that the explanation was helpful to you. Indeed, the diameter of pipelines and pump characteristics are critical factors in the efficiency of a piping system. It's great that you're considering your options and seeking professional recommendations for your property. Getting a proper water well pump installation with the right materials can make a big difference in the performance and longevity of your system. Best of luck with your project!