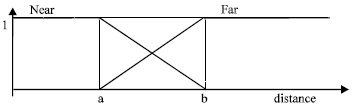
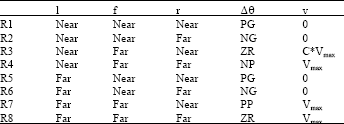
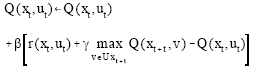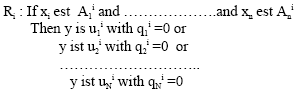Research Article
Parameter Tuning of Fuzzy Subsets Inertia Influence in Navigation Case
Signals, Images and Speech Laboratory, B.P. 78 C.P. 14000, Ibn Khaldoun University Tiaret, Algeria
A. Benyettou
University of Sciences and Technology of Oran, B.P. 1505 M Naouer 3 1 Oran Algeria