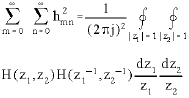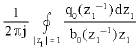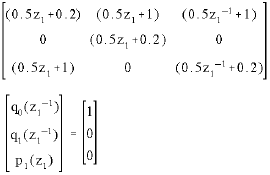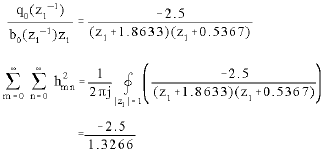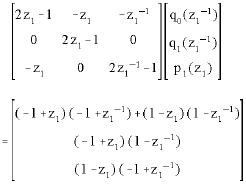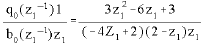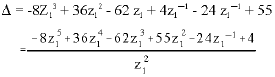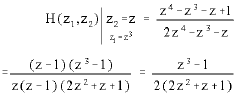Research Article
Stability Testing of 2-D Digital Filters Including Those Having Non-essential Singularities of the Second Kind
Applied University, P.O. Box 40 Al-Eys code 66141 Tafila, Jordan
P.S. Reddy
Department of Electronics and Communication Engineermg, SRM Engineering College, Chennai, Tamil Nadu, India