Research Article
An International Perspective on Business Cycle Asymmetry: Evidence from Non-parametric Analysis
Steven Cook Department of Economics, University of Wales Swansea, Singleton Park, Swansea S�2 8PP, Wales, TX.
Interest in the possibility of the business cycle displaying asymmetric behaviour has a long history in economics. Following the early studies of Mitchell[1], Keynes[2] and Burns and Mitchell[3], it has typically been suggested that asymmetry exists in the form of recessionary periods being shorter and more volatile than expansionary periods. More recently, formal tests have been employed to evaluate this proposition. A feature of this recent literature is the examination of cyclical asymmetry via application of Sichel's[4] moment-based tests. Following this approach, a detrending filter is applied to data to derive the underlying cyclical component of a time series, before Sichel's tests are employed[5-7]. In the present paper, this approach to examining business cycle asymmetry is extended in two ways. First, a much larger range of economies is examined than has previously been considered. In the present paper, national output is examined for 152 economies to provide a more complete analysis of asymmetry at an international level. Second, a non-parametric test recently introduced to the economics literature by Verbrugge[8] is employed to overcome noted problems with the moment-based tests of Sichel[4]. In particular, Mills[7] has noted that the results obtained from application of Sichel’s[4] tests can be biased by the presence of outliers in data. Consequently, when considering to national output for 22 OECD economies, Mills[7] applies the tests to a trimmed sample with detected outliers removed. In contrast, the non-parametric Triples test of Randles et al.[9] applied here has been found to be both robust to outliers and possess high power[10]. Therefore the present application of an alternative test to a large sample of economies complements the recent analysis of Mills[7] in which an absence of cyclical asymmetry at an international level was noted using a longer run of data for a more limited number of economies. Should asymmetry be uncovered, it will have a number of obvious implications for economic analysis. If the sizes of expansionary peaks and recessionary troughs, or the speeds at which they are approached, differ this will clearly have consequences for the implementation and impact of economic policy. At another level, detection of asymmetry will have implications for the specification of econometric models (which are typically linear and symmetric in nature), the understanding of economic behaviour and may also aid in the comparison and evaluation of alternative economic theories.
The data examined in this paper are annual observations on real, per capita GDP over the period 1970 to 2001. The data are obtained from the International Monetary Fund’s World Economic Outlook and cover 28 ‘advanced’ and 124 ‘developing and transition’ economies.
Testing for cyclical asymmetry
Detrending: To examine whether cyclical asymmetry is present, the cyclical component of GDP has to be derived for each of the economies considered. Following the standard approach in the literature, the cyclical component of the natural logarithm of per capita GDP is derived via application of a filter. Therefore, denoting the natural logarithm of real, per capita GDP for economy yi,t, the cyclical component of the series can be expressed as:
| (1) |
where τi,t is the trend underlying yi,t. Again, following the standard approach in the literature, the Hodrick-Prescott (HP)[11] filter is employed to derive τi,t. Essentially, subtraction of the HP trend allows the data examined to be filtered to isolate movements corresponding to business cycle fluctuations. Although numerous detrending procedures exist[12,13] the HP filter has a number of attractive features and advantages over its rivals in the present context. In particular, because of its linear structure, the HP filter will not induce spurious asymmetry in the derived cyclical components. Using the above notation, the HP filter derives a smooth trend τi,t as the solution to the following convex minimisation problem:
| (2) |
where L is the lag operator and λ is the smoothing parameter. It can be seen from the structure of HP filter that the extreme values of λ = {0,∞} result in the derived trend equaling the original series yi,t and a linear trend, respectively. Previously, the choice of the appropriate value of λ to employ in practice for annual data has not been well defined. However, the recent research of Ravn and Uhlig[14] presents convincing arguments for the adoption of 6.25 as the optimal value of the smoothing parameter λ. It is this value that is adopted here.
The triples test: Despite their frequent application in the economics literature, the moment-based tests of Sichel[4] are problematic as they are sensitive to outliers. It is therefore possible to draw misleading inferences from the application of these tests as a result of a single or a small number of unusual observations. In contrast, the alternative non-parametric Triples test of Randles et al.[9] has been shown to be robust to outliers and also possess high power[9,10]. It is for these reasons that its recent introduction to economics literature by Verbrugge[8] is to be welcomed. The mechanics of the Triples test can be explained as follows.
Consider a sample containing N observations of the variable X. The sample contains ![]() combinations of possible ‘triples’, or sets of three observations. To analyse asymmetry, the distance between the middle value and the two extreme values can be examined for each triple. The triple (Xi, Xj, Xk), where 1 ≤ I ≠ j ≠ k ≤ N, is therefore skewed to the right (left) if the middle observation is closer to the smallest (largest) value than the largest (smallest). Considering the function f* (Xi, Xj, Xk) defined as follows:
combinations of possible ‘triples’, or sets of three observations. To analyse asymmetry, the distance between the middle value and the two extreme values can be examined for each triple. The triple (Xi, Xj, Xk), where 1 ≤ I ≠ j ≠ k ≤ N, is therefore skewed to the right (left) if the middle observation is closer to the smallest (largest) value than the largest (smallest). Considering the function f* (Xi, Xj, Xk) defined as follows:
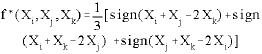 | (3) |
where:
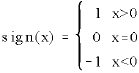 | (4) |
the triple (Xi, Xj, Xk) is a right triple if f * (Xi, Xj, Xk) = 1/3, while a left triple is given by f * (Xi, Xj, Xk) = –1/3. Obviously f * (Xi, Xj, Xk) = 0 corresponds to a triple which is not skewed. The test proposed by Randles et al.[9] is based upon the estimated value:
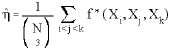 | (5) |
The Triples test of the null of symmetry (H0: η ≠ 0) against the alternative of asymmetry (H1: η ≠ 0) is then given by:
| (6) |
The numerator of this expression is provided in equation (5). The denominator is derived as below:
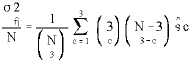 | (7) |
where:
| (8) |
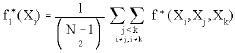 | (9) |
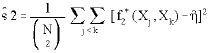 | (10) |
| (11) |
Randles et al.[9] showed that the test statistic T is asymptotically distributed as standard normal variate, with conventional critical values used to test the null hypothesis.
In the present study, the Triple test was employed to examine two possible forms of asymmetry. Application of the Triples test to the derived cyclical components (ci,t ) of GDP for each economy allows possible asymmetry to be uncovered in the form of a difference in the size of cyclical peaks and troughs. Therefore, if ![]() is found to be positive and significant, this indicates that the business cycle peaks are higher than troughs are deep. In contrast, a negative and significant value of
is found to be positive and significant, this indicates that the business cycle peaks are higher than troughs are deep. In contrast, a negative and significant value of ![]() indicates that the business cycle troughs are high. Asymmetry in the form of a difference in the size of peaks and troughs is referred to as deepness. However, asymmetry can also be considered in terms of the speeds at which peaks and troughs are approached. This possibility can be explored via application of the Triples test to the first differences of the cyclical components (Δci,t = ci,t - ci,t-1). Again, the significance and sign of
indicates that the business cycle troughs are high. Asymmetry in the form of a difference in the size of peaks and troughs is referred to as deepness. However, asymmetry can also be considered in terms of the speeds at which peaks and troughs are approached. This possibility can be explored via application of the Triples test to the first differences of the cyclical components (Δci,t = ci,t - ci,t-1). Again, the significance and sign of ![]() determines whether asymmetry is present and the form it takes. If
determines whether asymmetry is present and the form it takes. If ![]() is found to be positive and significant, this indicates that peaks are approached more rapidly than troughs. Conversely, a significant, negative statistic indicates the opposite, with troughs approached more rapidly than peaks. To determine the significance of the calculated triples test statistics (
is found to be positive and significant, this indicates that peaks are approached more rapidly than troughs. Conversely, a significant, negative statistic indicates the opposite, with troughs approached more rapidly than peaks. To determine the significance of the calculated triples test statistics (![]() ) , two-sided p-values are derived and reported. Evidence of asymmetry is noted
) , two-sided p-values are derived and reported. Evidence of asymmetry is noted ![]() is found to be significant at the 10% level (p-value≤0.1).
is found to be significant at the 10% level (p-value≤0.1).
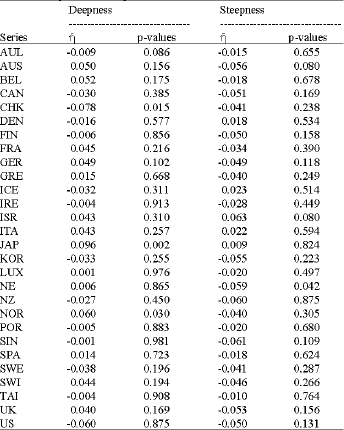
Considering the results for the advanced economies, evidence of deepness is found for China (Hong Kong), Germany, Japan and Norway, although in the case of Germany significance is marginal. For these economies, the calculated measure of asymmetry (![]() ) is negative for China, but positive for the other three economies. This indicates that while business cycle troughs are deeper than peaks are high for China, the reverse is true for Germany, Japan and Norway. From inspection of the results in Table 1, it can be seen that no other advanced economies display evidence of significant deepness. Turning to the results for steepness, significant evidence of steepness is uncovered for the following advanced economies: Austria, Israel and The Netherlands. For Austria and The Netherlands, the negative values of
) is negative for China, but positive for the other three economies. This indicates that while business cycle troughs are deeper than peaks are high for China, the reverse is true for Germany, Japan and Norway. From inspection of the results in Table 1, it can be seen that no other advanced economies display evidence of significant deepness. Turning to the results for steepness, significant evidence of steepness is uncovered for the following advanced economies: Austria, Israel and The Netherlands. For Austria and The Netherlands, the negative values of ![]() indicate that business cycle troughs are approached more rapidly than peaks, while the converse is true for Israel. No other economies possess significant steepness (Table 2).
indicate that business cycle troughs are approached more rapidly than peaks, while the converse is true for Israel. No other economies possess significant steepness (Table 2).
| Table 1: | Deepness and steepness tests for advanced economies |
 | |
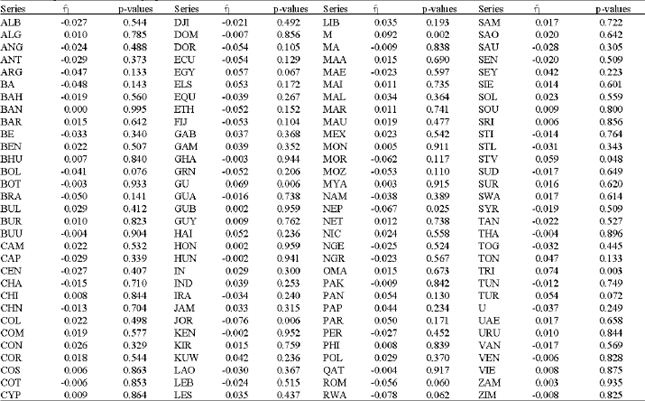
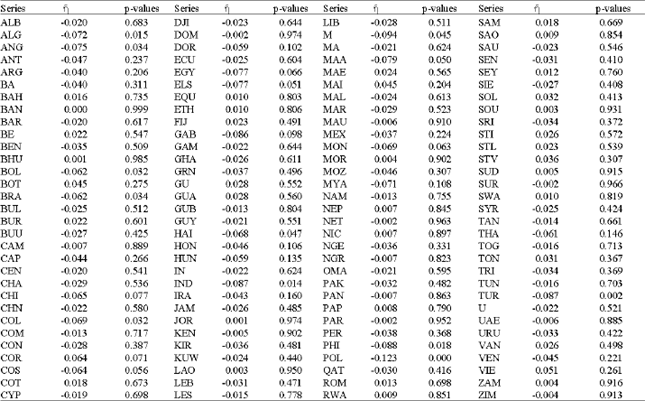
Considering the developing and transition economies, significant deepness is found for the following economies: Bolivia, The Dominican Republic, Egypt, Fiji, Guatemala, Jordan Madagascar, Nepal, Romania, Rwanda, St. Vincent and Grenadines and Turkey. However, it should be noted that the evidence for The Dominican Republic and Fiji is marginal. From inspection of sign of ![]() , it can be inferred that cyclical troughs are deeper than peaks are high for all of the above economies with the exception of Guatemala, Madagascar, St. Vincent and Grenadines and Turkey where peaks are larger than troughs. The complete set of results from the application of deepness tests to the developing and transition economies are contained in Table 2. The results for steepness indicate presence of asymmetry for Algeria, Angola, Bolivia, China (Mainland), Columbia, Congo republic, Costa Rica, Egypt, Haiti, Honduras, Indonesia, Madagascar, Malaysia, Philippines, Poland and Turkey. For each of these economies a negative value of
, it can be inferred that cyclical troughs are deeper than peaks are high for all of the above economies with the exception of Guatemala, Madagascar, St. Vincent and Grenadines and Turkey where peaks are larger than troughs. The complete set of results from the application of deepness tests to the developing and transition economies are contained in Table 2. The results for steepness indicate presence of asymmetry for Algeria, Angola, Bolivia, China (Mainland), Columbia, Congo republic, Costa Rica, Egypt, Haiti, Honduras, Indonesia, Madagascar, Malaysia, Philippines, Poland and Turkey. For each of these economies a negative value of ![]() is observed indicating that troughs are approached more rapidly than peaks. This consistency in the form of asymmetry is interesting as it corresponds to the form of asymmetry considered in the early business cycle literature with sharp declines into recessionary periods. The complete set of results from the application of the Triples test of steepness to the developing and transition economies are presented in Table 3.
is observed indicating that troughs are approached more rapidly than peaks. This consistency in the form of asymmetry is interesting as it corresponds to the form of asymmetry considered in the early business cycle literature with sharp declines into recessionary periods. The complete set of results from the application of the Triples test of steepness to the developing and transition economies are presented in Table 3.
| Table 2: | Deepness tests for developing and transition economies |
 | |
| Table 3: | Steepness tests for developing and transition economies |
 | |
In this study business cycle asymmetry has been examined using a range of economies. In contrast to previous studies, a recently proposed non-parametric test has been employed which is robust to outliers. In a further development of the literature, a larger range of economies has been examined than has previously been considered. The results of the analysis have show asymmetry to exist in a number of different forms. The analysis has also shown developing and transitional economies to possess asymmetry with the relative sizes of peaks and troughs and the speeds at which they are approached found to differ. As the presence of asymmetry has implications for economic policy, the understanding of economic behaviour and the specification of econometric models, the present results illustrating the existence of asymmetry for a number of economies have clear implications.