Research Article
Research on a New Type of Rotating Machine
Mechanical Engineering Department, Tafila Applied University College, Al-Balqa Applied University, Jordan
The problem of building some high -performance rotating working machines or prime movers is a current issue. The literature[1,2] presents some constructive solutions, which have certain disadvantages, such as: the constructive solution is complicated and consequently hard to implement from a technological point of view during operation, the mechanical friction produces big losses the motor momentum received (or yielded) by the machine shaft is not entirely used to increase the fluid pressure (or to produce mechanical energy). The constructive solution for a new type of machinery (N.T.M.) ensures the transformation of the shaft into a useful effect with minimum losses. No special technologies are required to build such a machine and additionally, the machine proves to be highly reliable during operation. The power exchanged by the N.T.M. with outside can be: required from the outside when the N.T.M. functions as a working machine (i.e. pump, fan, compressor) supplied to the outside when the N.T.M. functions as a prime mover (i.e. steam engine, pneumatic motor, hydrostatic motor). Next, a relation is established for the calculation of the N.T.M. theoretical power; then, the dependence between power and N.T.M. functioning and constructive parameters will be locked into.
The calculation of N.T.M. driving power: Figure 1 displays the constructive solution and operating principle of the N.T.M. as a working machine. The two rotors A and B are tangent. They have a synchronous rotation movement, which is ensured through providing some teeth on the rotor lateral surface, and providing two geared wheels outside the machine which are attached to shafts E and F (Fig. 1b). The fluid aspired (Fig. 1a) is carried towards discharge and after a 90 degree rotation movement of either rotor, the situation becomes the one shown in Fig. 1b. After another rotation of 180 degrees, the fluid, which is its useful volume Vu (Fig. 1c), i.e. in the space between pistons 3' and 4' will be carried to the discharge point.
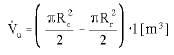 | (1) |
where; Rc = cylinder inside radius [m]
Rr = rotor radius [m]
l= rotor length [m]
With every complete full rotation of the shaft, two volumes (Vu) will be carried from the intake to the discharge and then:
| (2) |
It can be noticed that:
| (3) |
where; z = rotor height [m] Relations (2) and (3) result in:
| (4) |
Or after reducing the relation:
| (5) |
The volumic fluid flow discharged by one rotor of the machine is expressed as:
| (6) |
Where; v = frequency [rot/s]
Since the N.T.M. has two identical rotors, the flow of the machine-circulated fluid will be:
| (7) |
Or
| (8) |
where; n = machine rotation [rot/min]
The theoretical power needed to drive the working machine is given by the relation (1):
| (9) |
In which Δp represents the total pressure increase achieved by the working machine between suction and discharge. Supposing the N.T.M. has two identical rotors and functions as a prime mover, the power supplied to the outside will be expressed by a similar relation which is established in a different manner [3]:
| (10) |
where; Δp represents the pressure difference between one and the other surface of the rotating piston. Hence it can be noticed that
| (11) |
A relation where the first three parameters are geometrical and the following two are functional. Relation (11) shows that there is a linear dependence between P and l, R, n , Δp the machine power varying proportionally with these parameters. Between P and z there emerges a second -degree function which will be analyzed next.
The influence of the rotating piston height on N.T.M. power
The semicylinder radius is limited: Next the focus is to mathematically determine the extreme values of function P' = f (z2), i.e. to establish the minimum and maximum power exchanged with the outside by a particular type of N.T.M. (Rc = ct). To this effect, relation (10) shall be as follows:
| (12) |
If, in relation (12) derivative P' = f (z) is worked out and it is equaled to zero, then:
| (13) |
Or
| (14) |
Relation (14) as shown above does not reveal any information. If relation (14) replaces
| (15) |
then it becomes
| (16) |
Relation Rc=0 implies that z=0, that is the power is minimal when z=0, a result which is natural from a technical point of view. When is the power maximal? To obtain another extreme of function P=f(z2), the following procedure should be followed: in relation (10) we replace:
| (17) |
| (18) |
therefore it results
| (19) |
If we work out derivative P'=f(z2) and equal it to zero, we obtain:
| (20) |
It results that:
| (21) |
Therefore, the power is maximal when the piston height is equal with the cylinder radius; this result is correct from a technical point of view but it is impossible to be implemented in practice. Replacing relation (21) within relation (19) the value of N.T.M. maximum power can be obtained
| (22) |
As for relation (22) it can be noticed that:
The volume of the cylinder (Fig. 1) is:
| (23) |
By inserting relation (23) into relation (22) we obtain:
| (24) |
| (25) |
A part (k<l) of the N.T.M. volume is crossed by the fluid, thus the result kV ntmv; appears as a flow; consequently is a well-known relation in the specialized literature [1,4].
| (26) |
Thus, for this type of machine, it is also confirmed that the power exchanged with the outside is in relation and conjunction with the flow and pressure increase (or decrease) between suction and discharge. Let us see what happens if we set a technically restrictive condition such as:
| (27) |
where k>2.
If, within relation (19) written as
| (28) |
we replace Rc = kz, then we obtain:
| (29) |
If we work out derivative P' = f(z) and equal it with zero, we got:
| (30) |
The result obtained from this relation is identical to the one shown in relation (21), i.e., the machine power becomes maximal if z=Rc.
The semicylinder radius is not limited: Relation (12) can be written in a different way, such as:
| (31) |
For a certain operating mode (n= ct, Δp = ct), on every meter of the rotor length we obtain
| (32) |
Since z>0, in relation (32) it can be noticed that function P' = f(z2) is defined positively and has only one extreme, more exactly a minimum (Fig. 2).
Comparison between N.T.M. and Roots compressor: From the Aerzener Machinenfabrik G.M.B.H. booklet we have chosen a Roots rotating piston blower with the following characteristics features:
volumic flow ![]()
pressure increase
Δp = 7 mH2O = 68670 N/m2
power P = 14 kW
rotation n = 1450 rot./min
For the N.T.M. the constructive dimensions are selected so as to obtain the same flow:
| (33) |
By replacing relations (33) within relation (8) we obtain:
 |
If we adopt the same pressure increase, the power needed to drive the N.T.M. will be:
P = Vm. Δ p = 0.113 • 68670 = 7759W |
A value which is also found in Fig. (2). This theoretical power divided to a N.T.M. yield of approximately 0.7 shows an actual driving power of 11 kW as compared to the Roots blower's 14 kW; this lower power is one of the N.T.M. advantages over the Roots type compressor.
Figure 3 displayed the two-lobe Roots compressor; the discontinuous line outlines the N.T.M. rotors. Either machine has the same distances between axes and the same dimensions for the semi-cylinders. To make the drawing easier, the N.T.M. sketch does not show the rotating pistons and their holes. The space taken by the pistons and their holes will compensate when the flow is calculated.
In Figure 3, for the upper semicylimder, with every 180-degree rotation, the fluid volume carried from intake towards discharge is diminished by the space taken by half of the superior lobe, by half of the upper rotor in the case of the N.T.M. respectively.
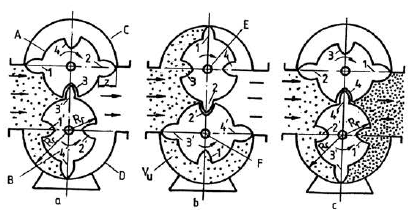 | |
| Fig. 1: | N.T.M. Outline: A, B rotors: C, D – Semi cylinders: E, F shafts: 1,2,3', 4' rotating pistons: 1 ', 2', 3, 4 holes where the rotating pistons penetrate |
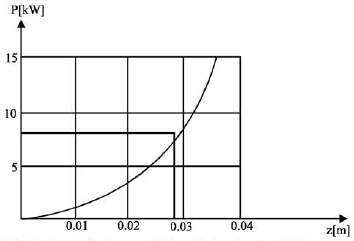 | |
| Fig. 2: | P =f (z2) for n = 1450 rot/min; Δp=7 mH2O. |
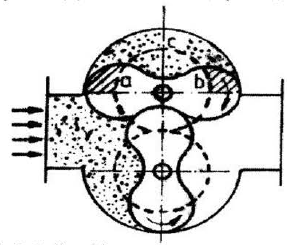 | |
| Fig. 3: | Outline of the roots compressor |
If we measure the areas, we can notice that the sum of the shaded areas is bigger than the abc area; this fact is obvious and clearly shown by the drawing too, if the contact area between the upper and lower lobes is carefully scrutinized. Consequently with every rotation, the fluid volume transported from intake to discharge by the Roots compressor will be smaller than the one supplied by the N.T.M.
From what has been presented above, we can distinguish two different cases:
Firstly, if the N.T.M. has a limited cylinder radius, then we can state that:
| • | The machine power is zero when z=Rc= 0 |
| • | The machine power is maximum when z=Rc. |
From a technical point of view the value z=Rc; cannot be achieved; from a constructive perspective one can choose z=k Rc; where k= 0.2-0.4. Since this type of machine has not been built yet, k values are tentative. II If the N.T.M. does not have a limited cylinder radius, then P= f (z2) is a strictly increasing function. In the case that the N.T.M. is used as a working machine, the fact that the motor momentum transmitted to the shaft is almost entirely employed to increase the fluid pressure shows that the proposed constructive solution is likely to be implemented in the future. Also, when the N.T.M. is used as a prime mover the thermal energy of the working fluid is transformed into a minimal-loose mechanical energy. No special technologies or materials are required to build such a machine.
Secondly, if it is miniaturized, the N.T.M. constructive solution can be used in a large number of fine mechanics domains (pneumatic micromotor, driving pump, etc) If we compare the N.T.M. with a two-lobe rotating Roots compressor, the formers advantages over the latter become obvious. The power needed to drive, to circulate the same fluid flow is lower
| • | When the main constructive dimensions (distances between axes, rotor length, semicylinder radius) are identical, the flow of the circulated fluid is higher. |
| • | The manufacturing technology is simpler. |
| • | Further research will have the objective of mathematically establishing the solution to the following issue: |
| • | What area does half of the superior lobe take and what area does half of the N.T.M. rotor occupies for the same value of the semicylinder radius in figure 3. |
| • | Thus, the flows of the two machines which are the object of the contrastive study can be compared in a mathematical way. |