Research Article
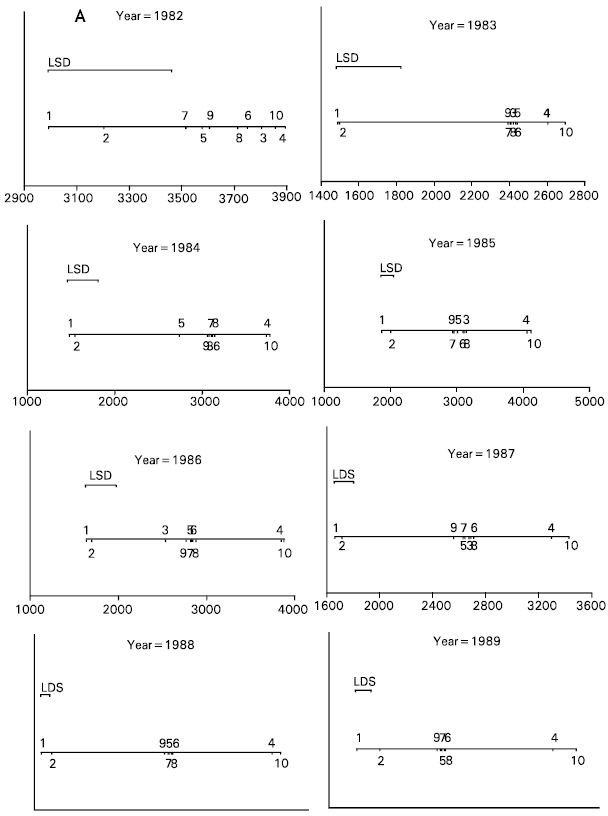
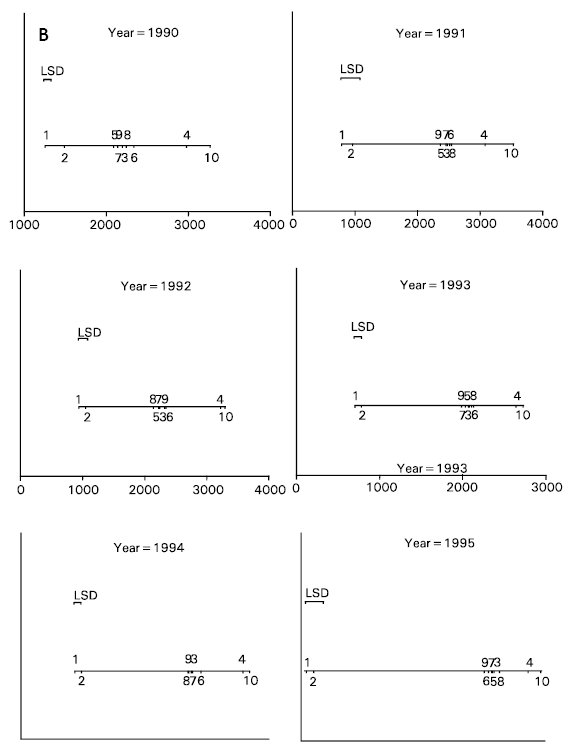
Visual Least-Significant-Difference and Visual Coefficient of Variation Methods for Screening of Experimental Treatments for Large Number of Response Variables
Bahauddin Zakariya University, Multan, Pakistan University of Kent at Canterbury, Kent, U.K.
G.M. Clarke
Bahauddin Zakariya University, Multan, Pakistan University of Kent at Canterbury, Kent, U.K.