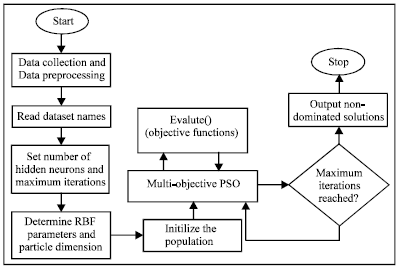
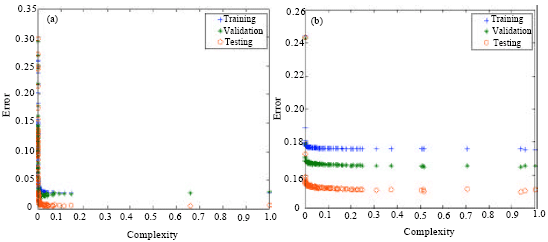
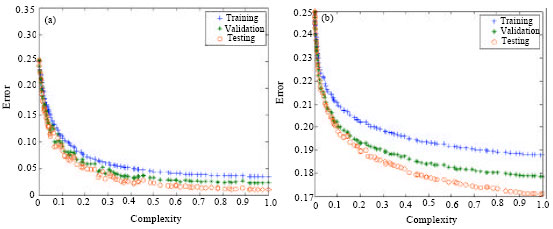
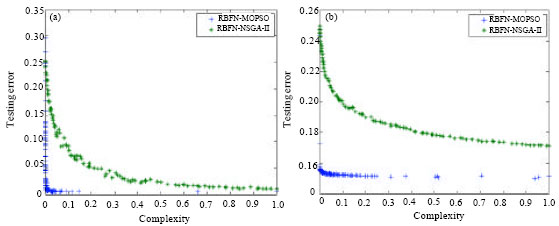
Research Article
Generalization Improvement of Radial Basis Function Network Based on Multi-Objective Particle Swarm Optimization
Soft Computing Research Group, Faculty of Computer Science and Information System, Universiti Teknologi Malaysia, 81310, Johor, Malaysia
S.M. Shamsuddin
Soft Computing Research Group, Faculty of Computer Science and Information System, Universiti Teknologi Malaysia, 81310, Johor, Malaysia