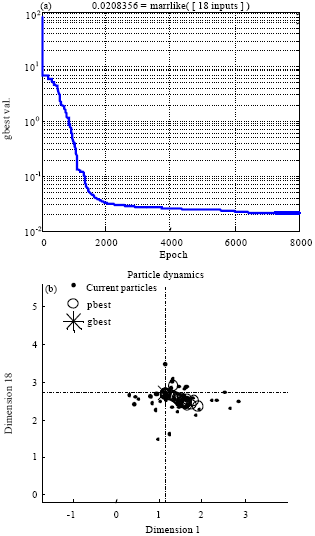
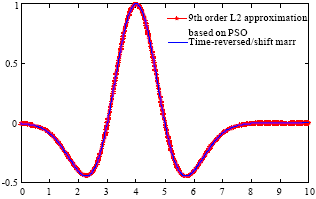
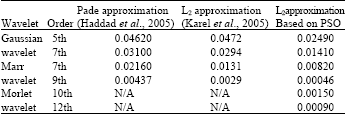
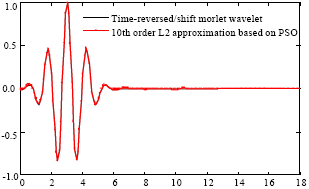
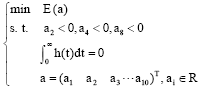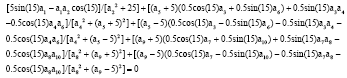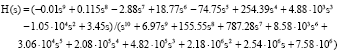Research Article
A PSO Method for Wavelet Approximation
College of Information and Communication Engineering, Hunan Institute of Science and Technology, 414006, Yueyang, China
Yigang He
College of Electrical and Automation Engineering, Hefei University of Technology, 230009, Hefei, China
Yichuang Sun
School of Electronic, Communication and Electrical Engineering, University of Hertfordshire, Hatfield ALl0 9AB, United Kingdom