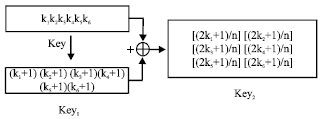
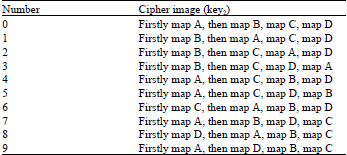
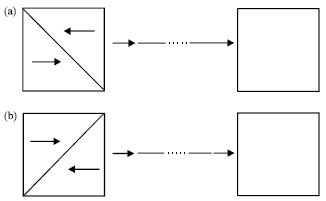
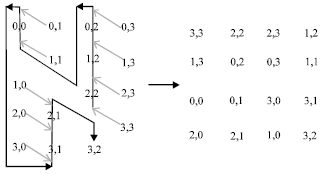
Research Article
A New Image Permutation Approach Using Combinational Chaotic Maps
College of Electrical and Information Engineering, Hunan Institute of Engineering, Xiangtan, 411105, China
Guixiang Zhang
Jianglu Machinery and Electronics Group Co., Ltd., Xiangtan, 411100, China