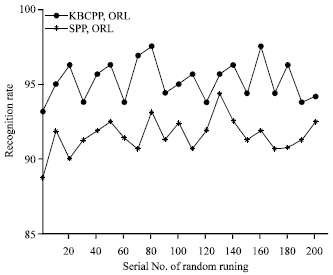
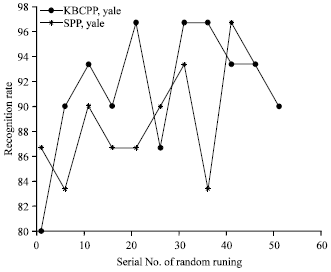
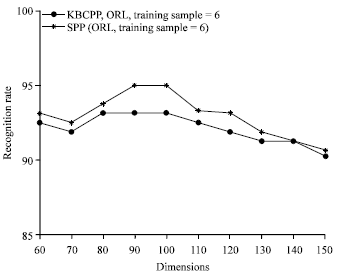
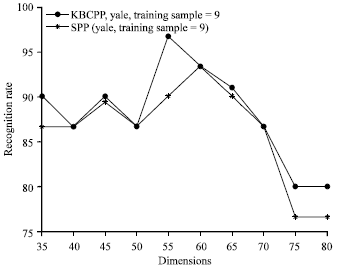
Research Article
A Kernel-based Collaborative Preserving Projection Based Face Recognition
School of Information Science and Engineering, Hunan University, Changsha, 410082, China
Zhiwei Kang
School of Information Science and Engineering, Hunan University, Changsha, 410082, China