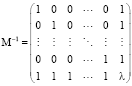
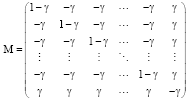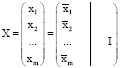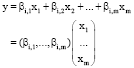Research Article
UC Secure Network Coding Against Pollution Attacks
School of Computer Communication of Lanzhou University of Technology, No. 287, Langongping Road, Qilihe District, Lanzhou, Gansu, People�s Republic of China
Wang Shuang
School of Computer Communication of Lanzhou University of Technology, No. 287, Langongping Road, Qilihe District, Lanzhou, Gansu, People�s Republic of China
Yuan Zhan-Ting
School of Computer Communication of Lanzhou University of Technology, No. 287, Langongping Road, Qilihe District, Lanzhou, Gansu, People�s Republic of China